【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,现给出以下四个结论:(1)AE=CF;(2)△EPF是等腰直角三角形;(3)S四边形AEPF=![]() S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )
S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )

A.1个B.3个C.![]() D.
D.![]()
参考答案:
【答案】D
【解析】
根据题意,容易证明△AEP≌△CFP,然后能推理得到选项A,B,C都是正确的,当EF=AP始终相等时,可推出![]() ,由AP的长为定值,而PF的长为变化值可知选项D不正确.从而求出正确的结论的概率.
,由AP的长为定值,而PF的长为变化值可知选项D不正确.从而求出正确的结论的概率.
解:∵AB=AC,∠BAC=90°,点P是BC的中点,
∴![]() ,
,![]() .
.
(1)在△AEP与△CFP中,
∵∠EAP=∠C=45°,AP=CP,∠APE=∠CPF=90°﹣∠APF,
∴△AEP≌△CFP
∴AE=CF.(1)正确;
(2)由(1)知,△AEP≌△CFP,
∴PE=PF,
又∵∠EPF=90°,
∴△EPF是等腰直角三角形.(2)正确;
(3)∵△AEP≌△CFP,同理可证△APF≌△BPE.
∴![]() .(3)正确;
.(3)正确;

(4)当EF=AP始终相等时,由勾股定理可得:![]()
则有:![]() ,
,
∵AP的长为定值,而PF的长为变化值,
∴![]() 与
与![]() 不可能始终相等,
不可能始终相等,
即EF与AP不可能始终相等,(4)错误,
综上所述,正确的个数有3个,
故正确的结论的概率是![]() .
.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知顶点为(-3,-6)的抛物线
 经过点(-1,-4),下列结论:①b2>4ac;②ax2+bx+c≥-6;③若点(-2,m),(-5,n)在抛物线上,则m>n;④关于x的一元二次方程
经过点(-1,-4),下列结论:①b2>4ac;②ax2+bx+c≥-6;③若点(-2,m),(-5,n)在抛物线上,则m>n;④关于x的一元二次方程 的两根为﹣5和﹣1,其中正确的有( )
的两根为﹣5和﹣1,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
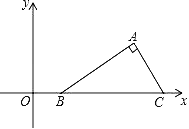
A. (﹣4,﹣2﹣
 ) B. (﹣4,﹣2+
) B. (﹣4,﹣2+ ) C. (﹣2,﹣2+
) C. (﹣2,﹣2+ ) D. (﹣2,﹣2﹣
) D. (﹣2,﹣2﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,且
,且 ,
,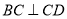 ,且
,且 ,请按照图中所标注的数据计算图中实线所围成的图形的面积
,请按照图中所标注的数据计算图中实线所围成的图形的面积 ______.
______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )

A. ①③B. ①②④C. ①③④D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个等式.例
如图1可以得到
 .请解答下列问题:
.请解答下列问题:
(1)根据图2,完成数学等式:
 = ;
= ;(2)观察图3,写出图3中所表示的等式: =____________.
(3)若
 、
、 、
、 ,且
,且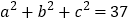 ,请利用(2)所得的结论求:
,请利用(2)所得的结论求: 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,点
,点 为线段
为线段 的中点,过点
的中点,过点 作一条直线分别与
作一条直线分别与 、
、 交于点
交于点 、
、 .点
.点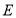 、
、 在直线
在直线 上,且
上,且 ,图中全等的三角形共有______对.
,图中全等的三角形共有______对.
相关试题

