【题目】已知△ABC和△ADE都是等腰直角三角形,点D是直线BC上的一动点(点D不与B、C重合),连接CE.
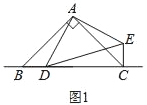
(1)在图1中,当点D在边BC上时,求证:BC=CE+CD;
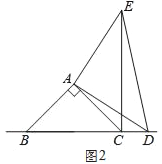
(2)在图2中,当点D在边BC的延长线上时,结论BC=CE+CD是否还成立?若不成立,请猜想BC、CE、CD之间存在的数量关系,并说明理由;
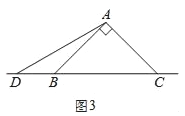
(3)在图3中,当点D在边BC的反向延长线上时,补全图形,不需写证明过程,直接写出BC、CE、CD之间存在的数量关系.
参考答案:
【答案】(1)见解析;(2)不成立,存在的数量关系为CE=BC+CD.理由见解析;(3)结论:CD=BC+EC.
【解析】
(1)在△ABD和△ACE中,由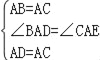 ,得△ABD≌△ACE(SAS),所以,BD=CE,
,得△ABD≌△ACE(SAS),所以,BD=CE,
可得BC=BD+CD=CE+CD;
(2)不成立,存在的数量关系为CE=BC+CD.同(1)△ABD≌△ACE(SAS),得BD=CE,所以BD=BC+CD,即CE=BC+CD;
(3)同(1)证△ABD≌△ACE(SAS),得BD=CE,所以CD=BC+BD=BC+CE.
(1)如图1中,
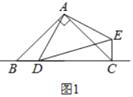
∵AB=AC,∠ABC=∠ACB=45°,AD=AE,∠ADE=∠AED=45°,
∴∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
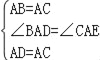 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD+CD=CE+CD;
(2)不成立,存在的数量关系为CE=BC+CD.
理由:如图2,由(1)同理可得,
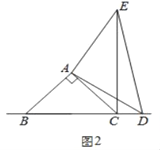
在△ABD和△ACE中,
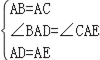 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BD=BC+CD,
∴CE=BC+CD;
(3)如图3,结论:CD=BC+EC.
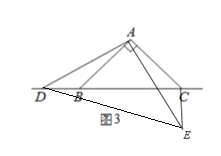
理由:由(1)同理可得,
在△ABD和△ACE中,
 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CD=BC+BD=BC+CE,
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子错误的是( )
A.cos40°=sin50°
B.tan15°tan75°=1
C.sin225°+cos225°=1
D.sin60°=2sin30° -
科目: 来源: 题型:
查看答案和解析>>【题目】某地下管道,若由甲队单独铺设,恰好在规定时间内完成;若由乙队单独铺设,需要超过规定时间15天才能完成,如果先由甲、乙两队合做10天,再由乙队单独铺设正好按时完成.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为5000元,乙队每天的施工费用为3000元,为了缩短工期以减少对居民交通的影响,工程指挥部最终决定该工程由甲、乙两队合做来完成,那么该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在下列各图中,点O为直线AB上一点,∠AOC=60°,直角三角板的直角顶点放在点处.
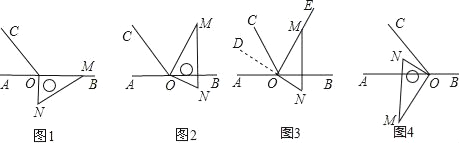
(1)如图1,三角板一边OM在射线OB上,另一边ON在直线AB的下方,则∠BOC的度数为 °,∠CON的度数为 °;
(2)如图2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线AB的下方,此时∠BON的度数为 °;
(3)请从下列(A),(B)两题中任选一题作答.
我选择: .
(A)在图2中,延长线段NO得到射线OD,如图3,则∠AOD的度数为 °;∠DOC与∠BON的数量关系是∠DOC ∠BON(填“>”、“=”或“<”);
(B)如图4,MN⊥AB,ON在∠AOC的内部,若另一边OM在直线AB的下方,则∠COM+∠AON的度数为 °;∠AOM﹣∠CON的度数为 °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国某部边防军小分队成一列在野外行军,通讯员在队伍中,数了一下他前后的人数,发现前面人数是后面的两倍,他往前超了6位战士,发现前面的人数和后面的人数一样.
(1)这列队伍一共有多少名战士?
(2)这列队伍要过一座320米的大桥,为安全起见,相邻两个战士保持相同的一定间距,行军速度为5米/秒,从第一位战士刚上桥到全体通过大桥用了100秒时间,请问相邻两个战士间距离为多少米(不考虑战士身材的大小)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:
指数运算
21=2
22=4
23=8
…
31=3
32=9
33=27
…
新运算
log22=1
log24=2
log28=3
…
log33=1
log39=2
log327=3
…
根据上表规律,某同学写出了三个式子:①log216=4,②log525=5,③log2
 =﹣1.其中正确的是( )
=﹣1.其中正确的是( )
A.①②
B.①③
C.②③
D.①②③
相关试题

