【题目】如图,以![]() 边为直径的⊙
边为直径的⊙![]() 经过点
经过点![]() ,
, ![]() 是⊙
是⊙![]() 上一点,连结
上一点,连结![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
, ![]() .
.
(1)试判断![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若点![]() 是弧
是弧![]() 的中点,已知
的中点,已知![]() ,求
,求![]() 的值.
的值.

参考答案:
【答案】(1)![]() 是⊙
是⊙![]() 的切线.证明见解析;(2)8.
的切线.证明见解析;(2)8.
【解析】试题分析:(1)连结OP,根据圆周角定理可得∠AOP=2∠ACP=120°,然后计算出∠PAD和∠D的度数,进而可得∠OPD=90°,从而证明PD是⊙O的切线;
(2)连结BC,首先求出∠CAB=∠ABC=∠APC=45°,然后可得AC长,再证明△CAE∽△CPA,进而可得![]() ,然后可得CECP的值.
,然后可得CECP的值.
试题解析:(1)如图, ![]() 是⊙
是⊙![]() 的切线.证明如下:
的切线.证明如下:
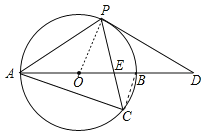
连结OP,
∵∠ACP=60°,
∴∠AOP=120°,
∵OA=OP,
∴∠OAP=∠OPA=30°,
∵PA=PD,
∴∠PAO=∠D=30°,
∴∠OPD=90°,
∴PD是⊙O的切线.
(2)连结BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵C为弧AB的中点,
∴∠CAB=∠ABC=∠APC=45°,
∵AB=4,AC=ABsin45°=2![]() .
.
∵∠C=∠C,∠CAB=∠APC,
∴△CAE∽△CPA,
∴![]() ,
,
∴CPCE=CA2=(2![]() )2=8.
)2=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度
2013
2014
2015
2016
投入技改资金
 (万元)
(万元)2.5
3
4
4.5
产品成本
 (万元/件)
(万元/件)7.2
6
4.5
4
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2
 ,CD=
,CD= BC,请求出GE的长.
BC,请求出GE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王上周买进某种股票1000股,每股27元。

(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)若小王在本周五的收盘价将股票全部卖出,你认为他会获利吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形
 中,
中, 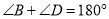 ,对角线
,对角线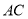 平分
平分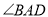 .
.(1)如图1,若
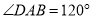 ,且
,且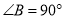 ,试探究边
,试探究边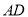 、
、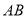 与对角线
与对角线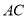 的数量关系并说明理由.
的数量关系并说明理由.(2)如图2,若将(1)中的条件“
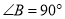 ”去掉,(1)中的结论是否成立?请说明理由.
”去掉,(1)中的结论是否成立?请说明理由.(3)如图3,若
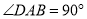 ,探究边
,探究边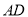 、
、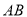 与对角线
与对角线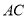 的数量关系并说明理由.
的数量关系并说明理由.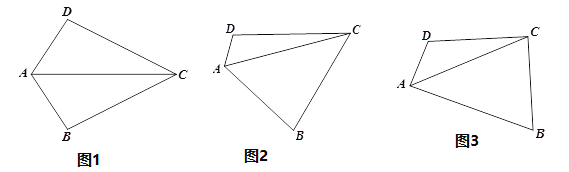
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4.若用想x,y表示直角三角形的两直角边(x>y),则下列四个说法:①
 ,②x-y=2,③2xy+4=49,④x+y=9其中说法正确的是( )
,②x-y=2,③2xy+4=49,④x+y=9其中说法正确的是( )
A. ①②B. ①②③④C. ②④D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校根据课程设置要求,开设了数学类拓展性课程. 为了解学生最喜欢的课程内容,随机抽取了部分学生进行问卷调查(每人必须且只选其中一项),并将统计结果绘制成如下统计图(不完整). 请根据图中信息回答问题:

(1)求
 的值.
的值. (2)补全条形统计图.
相关试题

