【题目】如图,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的有( )

①∠AOC=∠BOD=90°;②∠AOB=20°;③∠AOB=∠AOD-∠AOC;④∠AOB=![]() ∠BOD.
∠BOD.
A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】C
【解析】
根据已知条件和图形可以得到:∠AOD=∠BOC+2∠COD=110°,则∠AOB=∠COD=20°,由此可以对以下选项通过计算可以做出正确的判定.
解:如图,
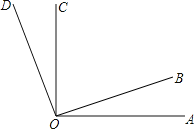
∵∠AOB=∠COD,∠AOD=110°,∠BOC=70°,
∴∠AOD=∠BOC+2∠COD=70°+2∠COD=110°,则∠AOB=∠COD=20°.
①∵∠AOB=∠COD,
∴∠BOC+∠AOB=∠BOC+∠COD=90°,即∠AOC=∠BOD=90°,故①正确;
②∠AOB=∠COD=20°.故②正确;
③由①知,∠AOC=∠BOD=90°,
∴∠AOB=∠AOD-∠BOD=∠AOD-∠AOC,
故③正确;
④∵∠AOB=20°,∠BOD=90°,
∴∠AOB=![]() ∠BOD.
∠BOD.
故④错误.
综上所述,正确的结论有3个.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进西装30件,衬衫45件,共用了39000元,其中西装的单价是衬衫的5倍。
(1)求西装和衬衫的单价各为多少元?
(2)商场仍需要购买上面的两种产品55件(每种产品的单价不变),采购部预算共支出32000元,财会算了一下,说:“如果你用这些钱共买这两种产品,那么账肯定算错了”请你用学过的方程知识解释财会为什么会这样说?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过O点作射线OC,使
 ,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为______度;
(2)在(1)旋转过程中,当旋转至图3的位置时,使得OM在∠BOC的内部,ON落在直线AB下方,试探究∠COM与∠BON之间满足什么等量关系,并说明理由.

-
科目: 来源: 题型:
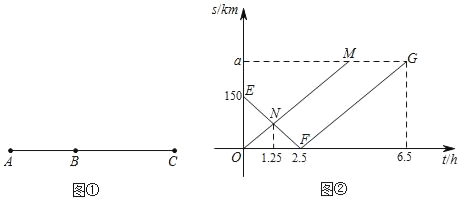
查看答案和解析>>【题目】如图①,A、B、C三地依次在一直线上,两辆汽车甲、乙分别从A、B两地同时出发驶向C地,如图②,是两辆汽车行驶过程中到C地的距离s(km)与行驶时间t(h)的关系图象,其中折线段EF﹣FG是甲车的图象,线段OM是乙车的图象.
(1)图②中,a的值为 ;点M的坐标为 ;
(2)当甲车在乙车与B地的中点位置时,求行驶的时间t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从全校1200名学生中随机选取一部分学生进行调查,调查情况:A:上网时间
 小时;B:1小时<上网时间
小时;B:1小时<上网时间  小时;C:4小时<上网时间
小时;C:4小时<上网时间  小时;D:上网时间>7小时.统计结果制成了如图统计图:
小时;D:上网时间>7小时.统计结果制成了如图统计图:
(1)参加调查的学生有人;
(2)请将条形统计图补全;
(3)请估计全校上网不超过7小时的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线

(1)该抛物线的对称轴是 , 顶点坐标;
(2)选取适当的数据填入下表,并在直角坐标系内描点画出该抛物线的图象;x
…
…
y
…
…

(3)若该抛物线上两点A(x1 , y1),B(x2 , y2)的横坐标满足x1>x2>1,试比较y1与y2的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:问题:某班在购买啦啦操比赛的物资时,准备购买红色、黄色,蓝色三种颜色的啦啦球,其颜色不同则价格不同,第一次买了15个红色啦啦球、7个黄色啦啦球、11个蓝色啦啦球共用1084元,第二次买了2个红色啦啦球、4个黄色啦啦球、3个蓝色啦啦球共用304元,试问第三次买了红、黄、蓝啦啦球各一个共需多少元?(假定三次购买红、黄、蓝啦啦球单价不变)
解:设购买红、黄、蓝啦啦球的单价分别为x、y、z元,依题意得:

上述方程组可变形为:

设x+y+z=m,2x+z=n,上述方程组又可化为:

①+4×②得:m= ,即x+y+z= ;
答:第三次购买红、黄、蓝啦啦球各一个共需 元.
阅读后,细心的你,可以解决下列问题:
某同学买13支黑笔、5支红笔、9个笔记本,共用去92.5元:如果买2支黑笔、4支红笔、3个笔记本,则共用去32元,试问只买一支黑笔、一支红笔、一个笔记本,共需多少钱?
相关试题

