【题目】已知等腰三角形ABC的底边长BC=20cm,D是AC上的一点,且BD=16cm,CD=12cm. 
(1)求证:BD⊥AC;
(2)求△ABC的面积.
参考答案:
【答案】
(1)证明:∵122+162=202,
∴CD2+BD2=BC2,
∴△BDC是直角三角形,
∴BD⊥AC
(2)解:设AD=xcm,则AC=(x+12 )cm,
∵AB=AC,
∴AB═(x+12 )cm,
在Rt△ABD中:AB2=AD2+BD2,
∴(x+12)2=162+x2,
解得x= ![]() ,
,
∴AC= ![]() +12=
+12= ![]() cm,
cm,
∴△ABC的面积S= ![]() BDAC=
BDAC= ![]() ×16×
×16× ![]() =
= ![]() cm2
cm2
【解析】(1)首先根据BD、CD、BC长可利用勾股定理逆定理证明BD⊥AC;(2)设AD=xcm,则AC=(x+12 )cm,在Rt△ABD中,利用勾股定理列出方程求解即可得到AB,进一步得到AC,再利用AC和AC边上的高列式计算即可得解.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
①abc>0
②4a+2b+c>0
③4ac﹣b2<8a
④
 <a<
<a<
⑤b>c.
其中含所有正确结论的选项是( )

A.①③ B.①③④ C.②④⑤ D.①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是40cm.求:
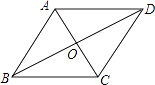
(1)两条对角线AC、BD的长度;
(2)菱形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于钝角α,定义它的三角函数值如下:
sinα=sin(180°﹣α),cosα=﹣cos(180°﹣α)
(1)求sin120°,cos120°,sin150°的值;
(2)若一个三角形的三个内角的比是1:1:4,A,B是这个三角形的两个顶点,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.(利用网格点和三角板画图)

(1)画出平移后的△A′B′C′.
(2)画出AB边上的高线CD;
(3)画出BC边上的中线AE;
(4)若连接BB′、CC′,则这两条线段之间的关系是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果上升8℃记作+8℃,那么﹣5℃表示( )
A. 上升5℃ B. 下降5℃ C. 上升3℃ D. 下降3℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠C=90°,a:b=3:4,运用计算器计算,∠A的度数(精确到1°)( )
A.30°
B.37°
C.38°
D.39°
相关试题

