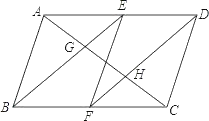
【题目】如图，在ABCD中，E、F分别为边AD、BC的中点，对角线AC分别交BE，DF于点G、H．求证：AG=CH．
【答案】证明见解析．
【解析】试题分析：根据平行四边形的性质得到AD∥BC，得出∠ADF=∠CFH，∠EAG=∠FCH，证出四边形BFDE是平行四边形，得出BE∥DF，证出∠AEG=∠CFH，由ASA证明△AEG≌△CFH，得出对应边相等即可．
试题解析：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠ADF=∠CFH，∠EAG=∠FCH，∵E、F分别为AD、BC边的中点，∴AE=DE=
AD，CF=BF=
BC，∴DE∥BF，DE=BF，∴四边形BFDE是平行四边形，∴BE∥DF，∴∠AEG=∠ADF，∴∠AEG=∠CFH，在△AEG和△CFH中，∵∠EAG=∠FCH，AE=CF，∠AEG=∠CFH，∴△AEG≌△CFH（ASA），∴AG=CH．
科目：初中数学 来源： 题型：
【题目】如图，在四边形OABC是边长为4的正方形，点P为OA边上任意一点（与点O、A不重合），连接CP，过点P作PM⊥CP交AB于点D，且PM=CP，过点M作MN∥AO，交BO于点N，连结ND、BM，设OP=t．
（1）求点M的坐标（用含t的代数式表示）；
（2）试判断线段MN的长度是否随点P的位置的变化而改变？并说明理由．
（3）当t为何值时，四边形BNDM的面积最小；
（4）在x轴正半轴上存在点Q，使得△QMN是等腰三角形，请直接写出不少于4个符合条件的点Q的坐标（用含t的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学校举行百科知识抢答赛，共有20道题，规定每答对一题记10分，答错或放弃记﹣4分，八年级一班代表的得分目标为不低于88分，则这个队至少要答对道题才能达到目标要求．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y=3x2向右平移1个单位，再向下平移2个单位，所得到的抛物线是（ ）
A.y=3（x﹣1）2﹣2
B.y=3（x+1）2﹣2
C.y=3（x+1）2+2
D.y=3（x﹣1）2+2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中,AD平分∠BAC，BD⊥AD于D，过D作DE∥AC交AB于点E.
（1）求证：E是AB的中点；
（2）若AB＝6，求线段DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列各组线段中，能成比例的是（ ）
A. 1cm，3cm，4cm，6cm B. 30cm，12cm，0.8cm，0.2cm
C. 0.1cm，0.2cm，0.3cm，0.4cm D. 12cm，16cm，45cm，60cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com