【题目】函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )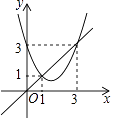
A.当1<x<3时,x2+(b﹣1)x+c<0
B.b+c=1
C.3b+c=6
D.b2﹣4c>0
参考答案:
【答案】A
【解析】解:∵抛物线与直线y=x相交于点(1,1),(3,3),
∴当1<x<3时,x2+bx+c<x,
即x2+(b﹣1)x+c<0,所以A选项符合题意;
把(1,1)代入y=x2+bx+c得1+b+c=1,
∴b+c=0,所以B选项错误;
把(3,3)代入y=x2+bx+c得9+3b+c=3,
∴3b+c=6,所以C选项不符合题意;
∵抛物线与x轴没有交点,
∴△=b2﹣4ac<0,所以D不符合题意.
所以答案是:A.
【考点精析】根据题目的已知条件,利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某商店出售了两个进价不同的书包,售价都是42元,其中一个盈利
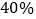 ,另一个亏损
,另一个亏损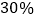 ,则在这次买卖中,商店的盈亏情况是
,则在这次买卖中,商店的盈亏情况是
A. 盈利
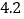 元B. 盈利6元C. 不盈不亏D. 亏损6元
元B. 盈利6元C. 不盈不亏D. 亏损6元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
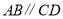 ,
,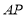 平分
平分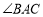 ,
,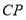 平分
平分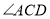 .求
.求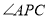 的度数;
的度数;请补全下列解法中的空缺部分.
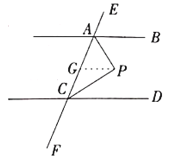
解:过点
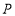 作
作 交
交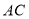 于点
于点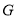
∵
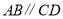 (___________)
(___________)∴_________
 (___________)
(___________)∵
 (___________)
(___________)∴
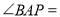 ___________(___________)
___________(___________)且
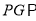 ______________(平行于同一直线的两直线也互相平行)
______________(平行于同一直线的两直线也互相平行)∴
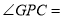 ____________(两直线平行,内错角相等)
____________(两直线平行,内错角相等)∵
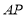 平分
平分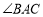 ,
,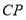 平分
平分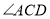 .
.∴
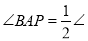 _____________,
_____________,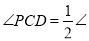 _________________.(___________)
_________________.(___________)∴
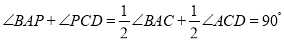 (___________)
(___________)∴
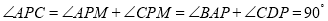
总结:两直线平行时,同旁内角的角平分线_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于
 BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )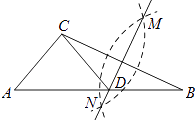
A.∠CAD=40°
B.∠ACD=70°
C.点D为△ABC的外心
D.∠ACB=90° -
科目: 来源: 题型:
查看答案和解析>>【题目】周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园,图中描述了小丽路上的情景,下列说法中正确的是_______.
①小丽在便利店停留时间为15分钟
②公园离小丽家的距离为2000米
③小丽从家到达公园共用时间20分钟
④小丽从家到便利店的平均速度为100米/分钟

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,圆的周长为4个单位长度在圆周的4等分点处标上字母A,B,C,D,先将圆周上的字母A对应的点与数轴上的原点重合,再将圆沿着数轴向右滚动,那么数轴上的1949所对应的点与圆周上字母
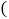
 所对应的点重合.
所对应的点重合.
A. AB. BC. CD. D
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:
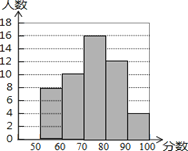
(1)本次选取参加测试的学生人数是 ___;
(2)学生“信息素养”得分的中位数落在 _____;
(3)若把每组中各个分数用这组数据的中间值代替(如30﹣40分的中间值为35分),则参加测试的学
生的平均分为多少分?
相关试题

