【题目】如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为°. 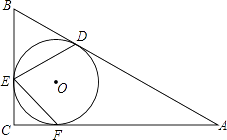
参考答案:
【答案】75
【解析】解:连接DO,FO, 
∵在Rt△ABC中,∠C=90°,∠B=60°
∴∠A=30°,
∵内切圆O与边AB、BC、CA分别相切于点D、E、F,
∴∠ODA=∠OFA=90°,
∴∠DOF=150°,
∴∠DEF的度数为75°.
所以答案是:75.
【考点精析】掌握圆周角定理和三角形的内切圆与内心是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,F分别是AB,CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列判断中,错误的是( )

A. ∠AEF=∠EFC B. ∠A=∠BCF C. ∠AEF=∠EBC D. ∠BEF+∠EFC=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】解决问题时需要思考:是否解决过与其类似的问题.小明从问题1解题思路中获得启发从而解决了问题2.
(1)问题1:如图①,在正方形ABCD中,E、F是BC、CD上两点,∠EAF=45°.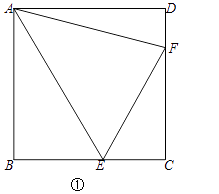
求证:∠AEF=∠AEB.
小明给出的思路为:延长EB到H,满足BH=DF,连接AH.请完善小明的证明过程.
(2)问题2:如图②,在等腰直角△ABC中,∠ACB=90°,AC=BC=4,D为AB中点,E、F是AC、BC边上两点,∠EDF=45°.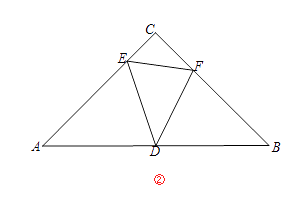
①求点D到EF的距离.
②若AE=a,则S△DEF=(用含字母a的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAP+∠APD=180°,∠1=∠2,求证:∠E=∠F.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师举了下面的例题:
例 1 等腰三角形 ABC 中,∠A=110°,求∠B 的度数.
例 2 等腰三角形 ABC 中,∠A=40°,求∠B 的度数.
张老师启发同学们进行变式,小敏编了如下一题:变式等腰三角形 ABC 中,∠A=70°,求∠B 的度数.
(1)请你解答以上的变式题.
(2)在等腰三角形 ABC 中,设∠A=x°,请用 x°表示出∠B 的度数;
(3)结合(1)(2),小敏发现,∠A 的度数不同,得到∠B 的度数的个数也可能不同,当∠B 有三种情况三个不同的度数时,讨论此时 x 的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC 中,∠A=90°,AB=AC,点 D 为 BC 的中点.
(1)点 E、F 分别为 AB、AC 上的中点,请按要求作出满足条件的△ABC 图形并证明:DE=DF;
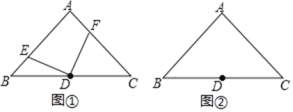
(2)如图①,若点 E、F 分别为 AB、AC 上的点,且 DE⊥DF,求证:BE=AF;
(3)若点 E、F 分别为 AB、CA 延长线上的点,且 DE⊥DF,那么 BE=AF 吗?请利用图②说明理由.
相关试题

