【题目】已知,在△ABC 中,∠A=90°,AB=AC,点 D 为 BC 的中点.
(1)点 E、F 分别为 AB、AC 上的中点,请按要求作出满足条件的△ABC 图形并证明:DE=DF;
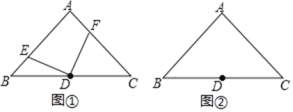
(2)如图①,若点 E、F 分别为 AB、AC 上的点,且 DE⊥DF,求证:BE=AF;
(3)若点 E、F 分别为 AB、CA 延长线上的点,且 DE⊥DF,那么 BE=AF 吗?请利用图②说明理由.
参考答案:
【答案】(1)见解析;(2)见解析;(3) BE=AF,见解析.
【解析】
(1)画图并证明△AED≌△AFD,可得DE=DF;
(2)如图①,证明△BDE≌△ADF,可得BE=AF;
(3)如图②,证明△EDB≌△FDA,可得BE=AF.
(1)如图,连接AD.

∵∠A=90°,AB=AC,点D为BC的中点,∴∠EAD=∠FAD.
∵点E、F分别为AB、AC上的中点,∴AE![]() AB,AF
AB,AF![]() AC.
AC.
在△AED和△AFD中,∵ ,∴△AED≌△AFD(SAS),∴DE=DF;
,∴△AED≌△AFD(SAS),∴DE=DF;
(2)连接AD,如图①所示.
∵∠BAC=90°,AB=AC,∴△ABC为等腰直角三角形,∠B=45°.
∵点D为BC的中点,∴AD![]() BC=BD,∠FAD=45°.
BC=BD,∠FAD=45°.
∵∠BDE+∠EDA=90°,∠EDA+∠ADF=90°,∴∠BDE=∠ADF.
在△BDE和△ADF中,∵ ,∴△BDE≌△ADF(ASA),∴BE=AF;
,∴△BDE≌△ADF(ASA),∴BE=AF;
(3)BE=AF.证明如下:
连接AD,如图②所示.
∵∠ABD=∠BAD=45°,∴∠EBD=∠FAD=135°.
∵∠EDB+∠BDF=90°,∠BDF+∠FDA=90°,∴∠EDB=∠FDA.
在△EDB和△FDA中,∵ ,∴△EDB≌△FDA(ASA),∴BE=AF.
,∴△EDB≌△FDA(ASA),∴BE=AF.
-
科目: 来源: 题型:
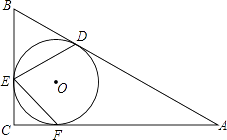
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAP+∠APD=180°,∠1=∠2,求证:∠E=∠F.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师举了下面的例题:
例 1 等腰三角形 ABC 中,∠A=110°,求∠B 的度数.
例 2 等腰三角形 ABC 中,∠A=40°,求∠B 的度数.
张老师启发同学们进行变式,小敏编了如下一题:变式等腰三角形 ABC 中,∠A=70°,求∠B 的度数.
(1)请你解答以上的变式题.
(2)在等腰三角形 ABC 中,设∠A=x°,请用 x°表示出∠B 的度数;
(3)结合(1)(2),小敏发现,∠A 的度数不同,得到∠B 的度数的个数也可能不同,当∠B 有三种情况三个不同的度数时,讨论此时 x 的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD.
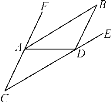
(1)判断∠FAB与∠C的大小关系,请说明理由;
(2)若∠C=35°,AB是∠FAD的平分线.
①求∠FAD的度数;
②若∠ADB=110°,求∠BDE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、B两点的坐标分别为(2,0)、(0,4),P是△AOB外接圆⊙C上的一点,且∠AOP=45°,则点P的坐标为 .

相关试题

