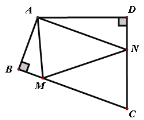
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,则∠AMN+∠ANM的角度为________.
参考答案:
【答案】140°
【解析】
作点A关于BC的对称点A′,关于CD的对称点A″,根据轴对称确定最短路线问题,连接A′A″与BC、CD的交点即为所求的点M、N,利用三角形的内角和定理列式求出∠A′+∠A″,再根据轴对称的性质和三角形的一个外角等于与它不相邻的两个内角的和可得∠AMN+∠ANM=2(∠A′+∠A″),然后计算即可得解.
如图,作点A关于BC的对称点A′,关于CD的对称点A″,连接A′A″与BC、CD的交点即为所求的点M、N.
∵∠BAD=110°,∠B=∠D=90°,∴∠A′+∠A″=180°﹣110°=70°,由轴对称的性质得:∠A′=∠A′AM,∠A″=∠A″AN,∴∠AMN+∠ANM=2(∠A′+∠A″)=2×70°=140°.
故答案为:140°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空,完成下列说理过程
如图,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数
解:因为∠AOB=90°.
所以∠BOC+∠AOC=90°
因为∠COD=90°
所以∠AOD+∠AOC=90°.
所以∠BOC=∠AOD. ( )
因为∠BOC=20°.
所以∠AOD=20°.
因为OA平分∠DOE
所以∠ =2∠AOD= °. ( )
所以∠COE=∠COD﹣∠DOE= °

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
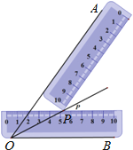
A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 三角形三条垂直平分线的交点到三个定点的距离相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】有A、B两种饮料,这两种饮料的体积和单价如表:
类型
A
B
单瓶饮料体积/升
1
2.5
单价/元
3
4
(1)小明购买A、B两种饮料共13升,用了25元,他购买A,B两种饮料个各多少瓶?
(2)若购买A、B两种饮料共36瓶,且A种饮料的数量不多于B种饮料的数量,则最少可以购买多少升饮料? -
科目: 来源: 题型:
查看答案和解析>>【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,
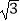 ≈1.7)
≈1.7) 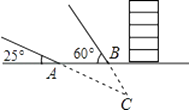
-
科目: 来源: 题型:
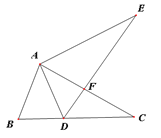
查看答案和解析>>【题目】如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠C=∠E,∠BAD=∠CAE,AC=AE.
(1)求证:△ABC≌△ADE;
(2)若∠B=60°,求证:△ABD是等边三角形.
-
科目: 来源: 题型:
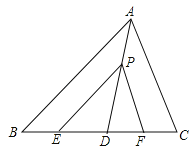
查看答案和解析>>【题目】如图,在△ABC中,点D,E,F在边BC上,点P在线段AD上,若PE∥AB,∠PFD=∠C,点D到AB和AC的距离相等.求证:点D到PE和PF的距离相等.
相关试题

