【题目】列方程解应用题:
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
参考答案:
【答案】甲工厂每天加工40件产品,乙工厂每天加工60件产品
【解析】试题分析:设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品.根据题目中的等量关系“甲工厂单独加工完成这批产品的天数﹣乙工厂单独加工完成这批产品的天数=10”,列出方程解方程即可.
试题解析:解:设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品,
依题意得![]() ,
,
解得:x=40.
经检验:x=40是原方程的根,且符合题意.所以1.5x=60.
答:甲工厂每天加工40件产品,乙工厂每天加工60件产品.
-
科目: 来源: 题型:
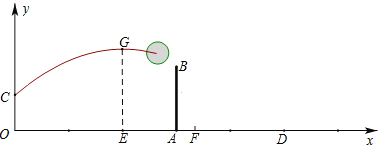
查看答案和解析>>【题目】2016年里约奥运会,中国女排的姑娘们在郎平教练指导下,通过刻苦训练,取得了世界冠军,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为3.2米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)的函数关系式.(不要求写自变量x的取值范围).
(2)在(1)的条件下,对方距球网0.5米的点F处有一队员,他起跳后的最大高度为3.1米,问这次她是否可以拦网成功?请通过计算说明.
(3)若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列解答中,填写适当的理由或数学式:

(1)∵∠A=∠CEF,( 已知 )
∴∥; ()
(2)∵∠B+∠BDE=180°,( 已知 )
∴∥;()
(3)∵DE∥BC,( 已知 )
∴∠AED=∠; ()
(4)∵AB∥EF,( 已知 )
∴∠ADE=∠ . () -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD
(1) 求证:E是OB的中点
(2) 若AB=8,求CD的长

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形纸片ABCD中,
 ,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过B,EF为折痕,当D′F
,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过B,EF为折痕,当D′F CD时,
CD时, 的值为__________.
的值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
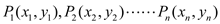 在函数
在函数 (x>0)的图象上,△OP1A1,△P2A1A2,△P3A2A3,……,△PnAn-1An……都是等腰直角三角形,斜边OA1,A1A2,……,An-1An,都在x轴上,则y1 + y2 + … + yn =___________.
(x>0)的图象上,△OP1A1,△P2A1A2,△P3A2A3,……,△PnAn-1An……都是等腰直角三角形,斜边OA1,A1A2,……,An-1An,都在x轴上,则y1 + y2 + … + yn =___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,

(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小,写出作法.
相关试题

