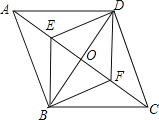
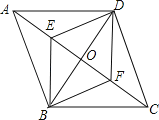
【题目】如图,O是菱形ABCD的对角线的交点,E、F分别是OA、OC的中点,下列结论:①四边形BFDE是菱形;②S四边形ABCD=EF×BD;③∠ADE=∠EDO;④△DEF是轴对称图形.其中正确的结论有( )
A.1个B.2个C.3个D.4个
参考答案:
【答案】C
【解析】
由菱形的性质可得AO=CO,BO=DO,AC⊥BD,由菱形的判定可判断①,由菱形的面积公式可判断②,由直角三角形的性质可判断③,由等腰三角形的性质可判断④.
解:∵四边形ABCD是菱形
∴AO=CO,BO=DO,AC⊥BD
∵E、F分别是OA、OC的中点
∴AE=EO=FO=CF,
∴EF=![]() AC
AC
∵EO=OF,BO=DO
∴四边形BEDF是平行四边形,且AC⊥BD
∴四边形BEDF是菱形,
故①正确
∵S四边形ABCD=![]() AC×BD
AC×BD
∴S四边形ABCD=EF×BD
故②正确
∵Rt△ADO中,DE是AO的中线
∴∠ADE≠∠EDO
故③错误
∵四边形BEDF是菱形,
∴△DEF是等腰三角形
∴△DEF是轴对称图形
故④正确
故正确的结论是①②④
故选:C.
-
科目: 来源: 题型:
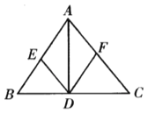
查看答案和解析>>【题目】如图,已知:AD是△ABC的角平分线,DE//AC交AB于E,DF//AB交AC于F,
(1)求证:四边形AEDF是菱形;
(2)当△ABC满足什么条件时,四边形AEDF是正方形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD//BC,
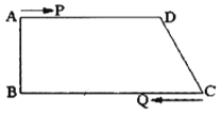
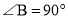 ,AD=24 cm,AB=8 cm, BC=26 cm,动点P从A开始沿AD边向D以1cm/s的速度运动;Q从点C开始沿CB边向B以3 cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动.
,AD=24 cm,AB=8 cm, BC=26 cm,动点P从A开始沿AD边向D以1cm/s的速度运动;Q从点C开始沿CB边向B以3 cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动.(1)当运动时间为t秒时,用含t的代数式表示以下线段的长: AP=________, BQ=__________;
(2)当运动时间为多少秒时,四边形PQCD为平行四边形?
(3)当运动时间为多少秒时,四边形ABQP为矩形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件不能判定四边形ABCD是矩形的是( )

A.∠DAB=∠ABC=∠BCD=90°B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DOD.AO=BO=CO=DO
-
科目: 来源: 题型:
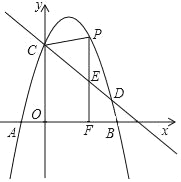
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B,与y轴交于C(0,3),直线y=
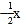 +m经过点C,与抛物线的另一交点为点D,点P是直线CD上方抛物线上的一个动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
+m经过点C,与抛物线的另一交点为点D,点P是直线CD上方抛物线上的一个动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.(1)求抛物线解析式并求出点D的坐标;
(2)连接PD,△CDP的面积是否存在最大值?若存在,请求出面积的最大值;若不存在,请说明理由;
(3)当△CPE是等腰三角形时,请直接写出m的值.
-
科目: 来源: 题型:
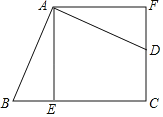
查看答案和解析>>【题目】如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△ABE绕着点A旋转后能与△ADF重合,若AF=5cm,则四边形ABCD的面积为_____.
-
科目: 来源: 题型:
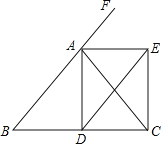
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,AD是角平分线,F为BA延长线上的一点,AE平分∠FAC,DE∥BA交AE于E.求证:四边形ADCE是矩形.
相关试题

