【题目】已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.
(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.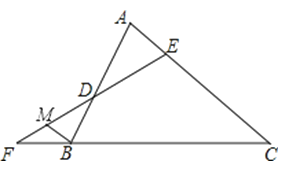
参考答案:
【答案】证明:(1)∵∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,
∴∠F+∠FEC=∠F+∠A+∠ADE,
∵∠ADE=∠BDF,
∴∠F+∠FEC=∠A+∠ABC,
∵∠A=∠ABC,
∴∠F+∠FEC=∠A+∠ABC=2∠A.
(2)∠MBC=∠F+∠FEC.
证明:∵BM∥AC,
∴∠MBA=∠A,、
∵∠A=∠ABC,
∴∠MBC=∠MBA+∠ABC=2∠A,
又∵∠F+∠FEC=2∠A,
∴∠MBC=∠F+∠FEC.
【解析】(1)根据三角形外角的性质,可得出∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,再根据∠A=∠ABC,即可得出答案;
(2)由BM∥AC,得出∠MBA=∠A,∠A=∠ABC,得出∠MBC=∠MBA+∠ABC=2∠A,结合(1)的结论证得答案即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.-1的相反数是1
B.-1的倒数是1
C.-1的平方根是±1
D.-1是无理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左边到右边的变形,属于因式分解的是( )
A.(x+1)(x-1)=x2-1B.x2-2x+1=x(x-2)+1
C.a(x-y)=ax-ayD.x2+2x+1=(x+1)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知P是△ABC内一点,连接PA,PB,PC,且PA=PB=PC,则P点一定是( )
A.△ABC的三条中线的交点
B.△ABC的三条内角平分线的交点
C.△ABC的三条高的交点
D.△ABC的三边的中垂线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(8x3﹣12x2﹣4x)÷(﹣4x)=( )
A. ﹣2x2+3xB. ﹣2x2+3x+1C. ﹣2x2+3x﹣1D. 2x2+3x+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】能作为直角三角形的三边长的一组数是( )
A. 2,3,4 B. 3,4,5 C. 6,7,8 D. 6,9,10
-
科目: 来源: 题型:
查看答案和解析>>【题目】“碧玉妆成一树高,万条垂下绿丝绦”. 每到春天,人们流连于柳绿桃红之间的同时也被漫天飞舞的柳絮所烦扰.据测定,柳絮纤维的直径约为0.0000105m,该数值用科学记数法表示为( )
A.1.05×105B.1.05×10-5C.-1.05×105D.105×10-7
相关试题

