【题目】如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(﹣5,0),且![]() ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
(1)求A、C两点的坐标;
(2)连接PA,用含t的代数式表示△POA的面积;
(3)当P在线段BO上运动时,是否存在一点P,使△PAC是等腰三角形?若存在,请写出满足条件的所有P点的坐标并求t的值;若不存在,请说明理由。

参考答案:
【答案】(1)A的坐标是![]() ,
,![]() 的坐标是
的坐标是![]() ;(2)当
;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)存在一点
;(3)存在一点![]() 、
、![]() 、
、![]() ,
,![]() 相对应的时间分别是
相对应的时间分别是![]() 、1.5、
、1.5、![]() 使
使![]() 是等腰三角形.
是等腰三角形.
【解析】
(1)根据偶次方和算术平方根的非负性得出![]() ,
,![]() ,求出即可;
,求出即可;
(2)分为三种情况:当![]() 时,
时,![]() 在线段
在线段![]() 上,②当
上,②当![]() 时,
时,![]() 和
和![]() 重合,③当
重合,③当![]() 时,
时,![]() 在射线
在射线![]() 上,求出
上,求出![]() 和
和![]() ,根据三角形的面积公式求出即可;
,根据三角形的面积公式求出即可;
(3)分为三种情况:①![]() 为顶角时,找出腰长关系便可解;②
为顶角时,找出腰长关系便可解;②![]() 为顶角时,找出腰长关系便可解;③
为顶角时,找出腰长关系便可解;③![]() 为顶角时,根据勾股定理可求得.
为顶角时,根据勾股定理可求得.
解:(1)![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 的坐标是
的坐标是![]() ,
,![]() 的坐标是
的坐标是![]() ;
;
(2)![]() ,
,
![]() ,
,
①当![]() 时,
时,![]() 在线段
在线段![]() 上,如图1,
上,如图1,

![]() ,
,![]() ,
,
![]() 的面积
的面积![]() ;
;
②当![]() 时,
时,![]() 和
和![]() 重合,此时
重合,此时![]() 不存在,即
不存在,即![]() ;
;
③当![]() 时,
时,![]() 在射线
在射线![]() 上,如备用图2,
上,如备用图2,
![]() ,
,![]() ,
,
![]() 的面积
的面积![]() ;
;
(3)![]() 在线段
在线段![]() 上运动使
上运动使![]() 是等腰三角形,分三种情况,
是等腰三角形,分三种情况,
①![]() 为顶角时,即
为顶角时,即![]() ,
,
![]() 为
为![]() 中垂线,
中垂线,
![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,![]() .
.
![]() ;
;
②![]() 为顶角时,
为顶角时,![]()
根据勾股定理可得,![]() ,
,
∵P在OB上,
![]() 点坐标为
点坐标为![]() ,
,![]()
![]() ;
;
③![]() 为顶角时,
为顶角时,![]() ,设
,设![]() ,
,
根据勾股定理,在![]() 中,
中,![]()
解得![]() ,
,
![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
综上,存在一点![]() 、
、![]() 、
、![]() ,
,![]() 相对应的时间分别是
相对应的时间分别是![]() 、1.5、
、1.5、![]() 使
使![]() 是等腰三角形.
是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
 若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率. 请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
请用树状图法或列表法,求恰好选中甲、乙两位同学的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=6,AD=8,沿BD折叠使点A到点A′处,DA′交BC于点F.
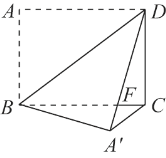
(1)求证:FB=FD;
(2)求证:CA′∥BD;
(3)求△DBF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距40km,甲、乙两人沿同一路线从A地到B地,甲骑自行车先出发,1.5h后乙乘坐公共汽车出发,两人匀速行驶的路程与时间的关系如图所示.
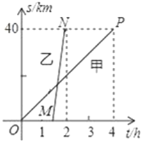
(1)求甲、乙两人的速度;
(2)若乙到达B地后,立即以原速返回A地.
①在图中画出乙返程中距离A地的路程y(km)与时间x(h)的函数图象,并求出此时y与x的函数表达式;
②求甲在离B地多远处与返程中的乙相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 、
、 两组卡片共
两组卡片共 张,
张, 中三张分别写有数字
中三张分别写有数字 ,
, ,
, ,
, 中两张分别写有
中两张分别写有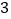 ,
, .它们除了数字外没有任何区别.
.它们除了数字外没有任何区别. 随机地从
随机地从 中抽取一张,求抽到数字为
中抽取一张,求抽到数字为 的概率;
的概率;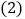 随机地分别从
随机地分别从 、
、 中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为
中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为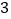 的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么? 如果不公平请你修改游戏规则使游戏规则对甲乙双方公平.
如果不公平请你修改游戏规则使游戏规则对甲乙双方公平. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定顾客消费
 元以上,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得
元以上,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得 元,
元, 元、
元、 元的购物券(转盘被等分成
元的购物券(转盘被等分成 个扇形).
个扇形). 顾客张吉祥消费
顾客张吉祥消费 元,他获得购物券的概率是多少?
元,他获得购物券的概率是多少? 他得到
他得到 元,
元, 元、
元、 元购物券的概率分别是多少?
元购物券的概率分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条长
 米,宽
米,宽 米的矩形草地上修三条小路,小路都等宽,除小路外,草地面积为
米的矩形草地上修三条小路,小路都等宽,除小路外,草地面积为 米2的
米2的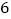 个矩形小块,则小路的宽度应为( )
个矩形小块,则小路的宽度应为( )
A.
 米或
米或 米 B.
米 B.  米 C.
米 C. 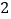 米 D.
米 D.  米
米
相关试题

