【题目】如图,在长方形ABCD中,AB=6,AD=8,沿BD折叠使点A到点A′处,DA′交BC于点F.
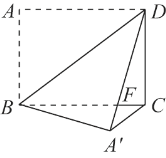
(1)求证:FB=FD;
(2)求证:CA′∥BD;
(3)求△DBF的面积.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据折叠的性质和矩形的性质可得∠ADB=∠BDA′,∠ADB=∠DBC,等量代换求出∠BDA′=∠DBC,然后根据等角对等边可得结论;
(2)首先求出FC=FA′,得到∠FCA′=∠FA′C,然后根据∠BFD=∠CFA′求出∠FBD=∠FCA′,利用平行线的判定可得结论;
(3)设FB=FD=x,则A′F=8-x,在Rt△BA′F中,利用勾股定理构造方程求出BF即可解决问题.
解:(1)由折叠的性质可得:∠ADB=∠BDA′,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠BDA′=∠DBC,
∴FB=FD;
(2)由折叠的性质可得:AD=A′D,
∵四边形ABCD是矩形,
∴AD=BC,
∴A′D=BC,
∵FB=FD,
∴FC=FA′,
∴∠FCA′=∠FA′C,
∵∠BFD=∠CFA′,
∴∠FBD+∠FDB=∠FCA′+∠FA′C,即2∠FBD=2∠FCA′,
∴∠FBD=∠FCA′,
∴CA′∥BD;
(3)∵AD=A′D=8,AB=A′B=6,FB=FD,∠BA′F=∠A=90°,
∴设FB=FD=x,则A′F=8-x,
在Rt△BA′F中,∵BA′2+A′F2=BF2,
∴![]() ,
,
解得:![]() ,即
,即![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商人制成了一个如图所示的转盘,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖励3元;若指针指向字母“C”,则奖励1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=﹣2x﹣3与y2=
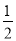 x+2.
x+2.(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3>
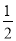 x+2的解集为多少?
x+2的解集为多少?(3)求两图象和y轴围成的三角形的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
 若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率. 请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
请用树状图法或列表法,求恰好选中甲、乙两位同学的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距40km,甲、乙两人沿同一路线从A地到B地,甲骑自行车先出发,1.5h后乙乘坐公共汽车出发,两人匀速行驶的路程与时间的关系如图所示.
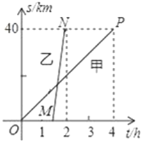
(1)求甲、乙两人的速度;
(2)若乙到达B地后,立即以原速返回A地.
①在图中画出乙返程中距离A地的路程y(km)与时间x(h)的函数图象,并求出此时y与x的函数表达式;
②求甲在离B地多远处与返程中的乙相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(﹣5,0),且
 ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.(1)求A、C两点的坐标;
(2)连接PA,用含t的代数式表示△POA的面积;
(3)当P在线段BO上运动时,是否存在一点P,使△PAC是等腰三角形?若存在,请写出满足条件的所有P点的坐标并求t的值;若不存在,请说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】
 、
、 两组卡片共
两组卡片共 张,
张, 中三张分别写有数字
中三张分别写有数字 ,
, ,
, ,
, 中两张分别写有
中两张分别写有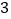 ,
, .它们除了数字外没有任何区别.
.它们除了数字外没有任何区别. 随机地从
随机地从 中抽取一张,求抽到数字为
中抽取一张,求抽到数字为 的概率;
的概率;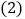 随机地分别从
随机地分别从 、
、 中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为
中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为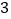 的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么? 如果不公平请你修改游戏规则使游戏规则对甲乙双方公平.
如果不公平请你修改游戏规则使游戏规则对甲乙双方公平.
相关试题

