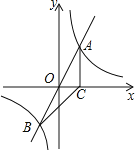
【题目】如图, 正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。
参考答案:
【答案】(1)k=2(2)D(![]() ,0)或(-
,0)或(-![]() ,0)
,0)
【解析】试题分析:(1)根据对称性可得OA=OB,从而可得△ACO的面积为1,由此可求出点A的坐标,然后运用待定系数法就可解决问题,
(2)先将y=2x与y=![]() 联立成方程组,求出A,B两点的坐标,由 O为线段AB的中点,
联立成方程组,求出A,B两点的坐标,由 O为线段AB的中点,
可得OD=![]() AB=OA,然后利用勾股定理求出OA的值,即可求出D点的坐标.
AB=OA,然后利用勾股定理求出OA的值,即可求出D点的坐标.
试题解析:(1)设点A的坐标为(m,n),
∵点A在直线y=2x上,
∴n=2m,
根据对称性可得OA=OB,
∴S△ABC=2S△ACO=2,
∴S△ACO=1,
∴![]() m2m=1,
m2m=1,
∴m=1(舍负),
∴点A的坐标为(1,2),
∴k=1×2=2,
(2)x轴上存在一点D,使△ABD为直角三角形,
将y=2x与y=![]() 联立成方程组得:
联立成方程组得:
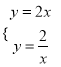 ,
,
解得: ![]() ,
,![]() ,
,
∴A(1,2),B(-1,-2),
当AD⊥BD时,如图,
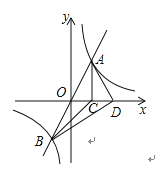
∵O为线段AB的中点,
∴OD=![]() AB=OA,
AB=OA,
∵A(1,2),
∴OC=1,AC=2,
由勾股定理得:OA=![]() =
=![]() ,
,
∴OD=![]() ,
,
∴D(![]() ,0),
,0),
根据对称性,当D为直角顶点,且D在x轴负半轴时,D(-![]() ,0),
,0),
故x轴上存在一点D,使△ABD为直角三角形,点D的坐标为(![]() ,0)或(-
,0)或(-![]() ,0).
,0).
-
科目: 来源: 题型:
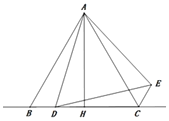
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AH⊥BC,垂足为H,D为直线BC上一动点(不与点B、C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)求证:BD=CE;
(2)若点D在线段BC上,问点D运动到何处时,AC⊥DE?请说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数.(直接写出结果,无需写出求解过程)


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的网格是正方形网格,则
 __________
__________ (点
(点 ,
, ,
, ,
, ,
, 是网格线交点).
是网格线交点).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想
 的值,并说明理由.
的值,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级两个班,各选派10名学生参加学校举行的“美丽绍兴乡土风情知识”大赛预赛各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级
最高分
平均分
中位数
众数
方差
八(1)班
100
m
93
93
12
八(2)班
99
95
n
93
8.4
(1)求表中m、n的值;
(2)依据数据分析表,有同学说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有同学说(2)班的成绩更好请您写出两条支持八(2)班成绩好的理由.
-
科目: 来源: 题型:
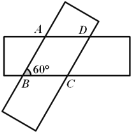
查看答案和解析>>【题目】如图,将两条宽度为3的直尺重叠在一起,使∠ABC=60°,则四边形ABCD的面积是_____________
相关试题

