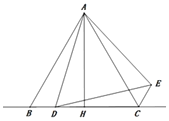
【题目】如图,在△ABC中,AB=AC,AH⊥BC,垂足为H,D为直线BC上一动点(不与点B、C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)求证:BD=CE;
(2)若点D在线段BC上,问点D运动到何处时,AC⊥DE?请说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数.(直接写出结果,无需写出求解过程)


参考答案:
【答案】(1)证明见解析;(2)当点D运动到BC中点(H点)时,AC⊥DE.理由见解析;(3)∠ADB的度数为20°或40°或100°.
【解析】
(1)由∠DAE=∠BAC证明∠BAD=∠CAE,再证明△BAD≌△CAE即可得到结论,
(2)利用等腰三角形的性质,证明∠CAH=∠CAE,再利用三线合一可得结论,
(3)分三种情形:①当点D在CB的延长线上时,∠ADB=40°; ②当点D在线段BC上时,最小角只能是∠DAB=20°,此时∠ADB=180°-20°-60°=100°. ③当点D在BC 延长线上时,最小角只能是∠ADB=20°;即可得到答案.
证明:(1)如图1.
∵∠DAE=∠BAC
∴∠BAD=∠CAE
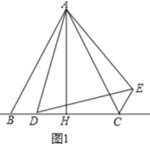
在△BAD和△CAE中,
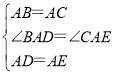 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)当点D运动到BC中点(H点)时,AC⊥DE
理由是:如图2.
∵AB=AC,AH⊥BC
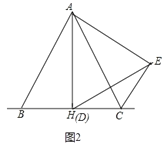
∴∠BAH=∠CAH
∵∠BAH=∠CAE,
∴∠CAH=∠CAE
∵AH=AE,
∴AC⊥DE.
(3)∠ADB的度数为20°或40°或100°.
理由如下:
①如图3中,当点D在CB的延长线上时,
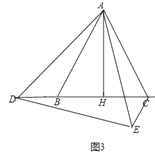
∵CE∥AB,
∴∠BAE=∠AEC,∠BCE=∠ABC.
∵△DAB≌△EAC,
∴∠ADB=∠AEC,∠ABD=∠ACE,
∴∠BAC=∠BAE+∠EAC=∠AEC+∠EAC=180°-∠ACE=180°-∠ABD=∠ABC=∠ACB,∴△ABC是等边三角形,
∴∠ABC=60°
∵△ABD中的最小角是∠BAD=20°,
则∠ADB=∠ABC-∠BAD=40°.
②当点D在线段BC上时,最小角只能是∠DAB=20°,
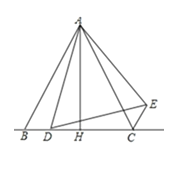
同理可得:∠ADB=180°-20°-60°=100°.
③当点D在BC延长线上时,最小角只能是∠ADB=20°,
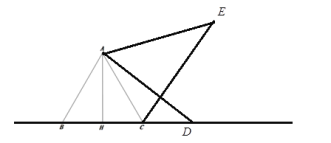
综上所述:满足条件的∠ABD的值为20°或40°或100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数
 的图象交
的图象交 轴、
轴、 轴分别于
轴分别于 两点,交直线
两点,交直线 于
于 。
。(1)求点
 的坐标;
的坐标;(2)若
 ,求
,求 的值;
的值;(3)在(2)的条件下,
 是线段
是线段 上一点,
上一点, 轴于
轴于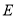 ,交
,交 于
于 ,若
,若 ,求
,求 点的坐标。
点的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC底边BC的长为4cm,面积为12cm,腰AB的垂直平分线交AB于点E,若点D为BC边的中点,M为线段EF上一动点,则△BDM的周长最小值为_________

-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月,某县突降暴雨,造成山体滑坡,桥梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1 000件帐篷与乙种货车装运800件帐篷所用车辆相等.
(1)求甲、乙两种货车每辆车可装多少件帐篷;
(2)如果这批帐篷有1 490件,用甲、乙两种汽车共16辆装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其余装满,求甲、乙两种货车各有多少辆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的网格是正方形网格,则
 __________
__________ (点
(点 ,
, ,
, ,
, ,
,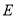 是网格线交点).
是网格线交点).
-
科目: 来源: 题型:
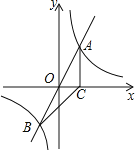
查看答案和解析>>【题目】如图, 正比例函数
 的图象与反比例函数
的图象与反比例函数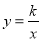 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。
相关试题

