【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
参考答案:
【答案】(1)y=![]() ;(2)20天;(3)5辆.
;(2)20天;(3)5辆.
【解析】
试题分析:(1)根据每天能运xm3,所需时间为y天的积就是1200m3,即可写出函数关系式;
(2)把x=12×5=60代入,即可求得天数;
(3)首先算出8天以后剩余的数量,然后计算出6天运完所需的拖拉机数,即可求解.
试题解析:(1)∵xy=1200,
∴y=![]() ;
;
(2)x=12×5=60,代入函数解析式得;y=![]() =20(天)
=20(天)
答:20天运完;
(3)运了8天后剩余的垃圾是1200-8×60=720m3.
剩下的任务要在不超过6天的时间完成则每天至少运720÷6=120m3,
则需要的拖拉机数是:120÷12=10(辆),
则至少需要增加10-5=5辆这样的拖拉机才能按时完成任务.
-
科目: 来源: 题型:
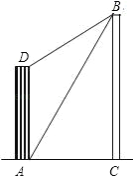
查看答案和解析>>【题目】大楼AD的高为10米,不远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D点测得塔顶B点的仰角为30°,求塔BC的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某储运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物运往青岛,这列货车可挂A、B两种不同规格的货厢50节.已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,按此要求安排A、B两种货厢的节数,有哪几种运输方案?请设计出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),将两块直角三角板的直角顶点C叠放在一起.
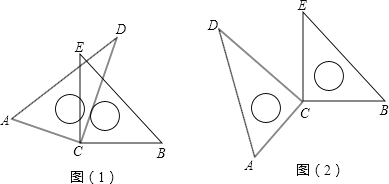
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】代数式x2+2x+7的值是6,则代数式4x2+8x﹣5的值是( )
A. ﹣9 B. 9 C. 18 D. ﹣18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下表:
n
1
2
3
4
…
y
2×1
4×3
6×5
8×7
试研讨这里的y与n的关系式,并指出其中的变量.
相关试题

