【题目】点Pm1,2m+1在第二象限,则m的取值范围是________;
若点Pa,a2在第四象限,则a的取值范围是________;
若点Pa,|a|3在x轴正半轴上,则a的值是__________.
参考答案:
【答案】![]() <m<1; 0<a<2; 3.
<m<1; 0<a<2; 3.
【解析】
根据:第一象限点的坐标特点为横坐标为正,纵坐标为正;第二象限点的坐标特点为横坐标为负,纵坐标为正;第三象限点的坐标特点为横坐标为负,纵坐标为负;第四象限点的坐标特点为横坐标为正,纵坐标为负.在x轴上的点纵坐标等于0.
(1)因为点Pm1,2m+1在第二象限,
所以,m1<0,2m+1>0,
解得![]() <m<1
<m<1
则m的取值范围是![]() <m<1;
<m<1;
(2)因为点Pa,a2在第四象限,
所以a>0,a2<0
解得0<a<2
则a的取值范围是0<a<2;
(3)若点Pa,|a|3在x轴正半轴上,
则a>0,|a|3=0
解得:a=3
故答案是:![]() <m<1 ;0<a<2 ;3.
<m<1 ;0<a<2 ;3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了拉动内需,全国各地汽车购置税补贴活动在2009年正式开始,某经销商在政策出台前一个月共售出某品牌汽车的手动型和自动型共960台,政策出台后的第一个月售出这两种型号的汽车共1228台,其中手动型和自动型汽车的销售量分别比政策出台前一个月增长30%和25%.
(1)在政策出台前一个月,销售的手动型和自动型汽车分别为多少台?
(2)若手动型汽车每台价格为8万元,自动型汽车每台价格为9万元.根据汽车补贴政策,政府按每台汽车价格的5%给购买汽车的用户补贴,问政策出台后的第一个月,政府对这1228台汽车用户共补贴了多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小孟同学将等腰直角三角板ABC(AC=BC)的直角顶点C放在一直线m上,将三角板绕C点旋转,分别过A,B两点向这条直线作垂线AD,BE,垂足为D,E.
(1)如图1,当点A,B都在直线m上方时,猜想AD,BE,DE的数量关系是 ;
(2)将三角板ABC绕C点按逆时针方向旋转至图2的位置时,点A在直线m上方,点B在直线m下方.(1)中的结论成立吗?请你写出AD,BE,DE的数量关系,并证明你的结论.
(3)将三角板ABC继续绕C点逆时针旋转,当点A在直线m的下方,点B在直线m的上方时,请你画出示意图,按题意标好字母,直接写出AD,BE,DE的数量关系结论 .

-
科目: 来源: 题型:
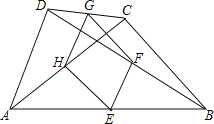
查看答案和解析>>【题目】如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
(1)判断四边形EFGH是何种特殊的四边形,并说明你的理由;
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )
A.①②③④
B.②③
C.①②④
D.①③④ -
科目: 来源: 题型:
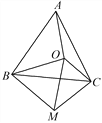
查看答案和解析>>【题目】如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?

相关试题

