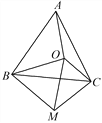
【题目】如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
参考答案:
【答案】(1)AO=CM (2)△OMC是直角三角形
【解析】试题分析:(1)先证明△OBM是等边三角形,得出OM=OB,∠ABC=∠OBC,由SAS证明△AOB≌△CMB,即可得出结论;
(2)由勾股定理的逆定理即可得出结论.
试题解析:解:(1)AO=CM.理由如下:
∵∠OBM=60°,OB=BM,∴△OBM是等边三角形,∴OM=OB=10,∠ABC=∠OBC=60°,
∴∠ABO=∠CBM.在△AOB和△CMB中,∵OB=OM,∠ABO=∠CBM,AB=BC,∴△AOB≌△CMB(SAS),∴OA=MC;
(2)△OMC是直角三角形;理由如下:
在△OMC中,OM2=100,OC2+CM2=62+82=100,∴OM2=OC2+CM2,∴△OMC是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装销售商在进行市场占有率的调查时,他最应该关注的是……………( )
A. 服装型号的平均数 B. 服装型号的众数
C. 服装型号的中位数 D. 最小的服装型号
-
科目: 来源: 题型:
查看答案和解析>>【题目】一射击运动员在一次射击练习中打出的成绩是(单位:环):7,8,9,8,6,8,10,7,这组数据的众数是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知O是坐标原点,点A的坐标是(5,0),点B是y轴正半轴上一动点,以OB,OA为边作矩形OBCA,点E,H分别在边BC和边OA上,将△BOE沿着OE对折,使点B落在OC上的F点处,将△ACH沿着CH对折,是点A落在OC上的G点处。
(1)求证:四边形OECH是平行四边形;
(2)如图2,当点B运动到使得点F,G重合时,判断四边形OECH的形状并说明理由;
(3)当点B运动到使得点F,G将对角线OC三等分时,求点B的坐标。

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校七年级 1500 名学生的身高情况,从中抽取了 300 名学生进行测量,这个样本的容量(即样本中个体的数量)是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点 P(3,-10)到 x 轴的距离为_____.
相关试题

