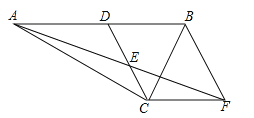
【题目】已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的长.
参考答案:
【答案】(1)证明见解析;(2)4.
【解析】试题分析:(1)先根据点E是CD的中点得出DE=CE,再由AB∥CF可知∠BAF=∠AFC,根据AAS定理可得出△ADE≌△FCE;
(2)根据直角三角形的性质可得出AD=CD=![]() AB,再由AB∥CF可知∠BDC=180°﹣∠DCF=180°﹣120°=60°,由三角形外角的性质可得出∠DAC=∠ACD=
AB,再由AB∥CF可知∠BDC=180°﹣∠DCF=180°﹣120°=60°,由三角形外角的性质可得出∠DAC=∠ACD=![]() ∠BDC=30°,进而可得出结论.
∠BDC=30°,进而可得出结论.
试题解析:(1)证明:∵点E是CD的中点,∴DE=CE.
∵AB∥CF,∴∠BAF=∠AFC.
在△ADE与△FCE中,∵∠BAF=∠AFC,∠AED=∠FEC,DE=CE,∴△ADE≌△FCE(AAS);
(2)解:由(1)得,CD=2DE,∵DE=2,∴CD=4.
∵点D为AB的中点,∠ACB=90°,∴AB=2CD=8,AD=CD=![]() AB.
AB.
∵AB∥CF,∴∠BDC=180°﹣∠DCF=180°﹣120°=60°,∴∠DAC=∠ACD=![]() ∠BDC=
∠BDC=![]() ×60°=30°,∴BC=
×60°=30°,∴BC=![]() AB=
AB=![]() ×8=4.
×8=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:
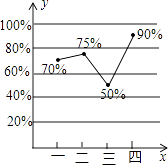
(1)若第一季度的汽车销售量为2100辆,求该季的汽车产量;
(2)圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤4).
(1)当t=3时,求足球距离地面的高度;
(2)当足球距离地面的高度为10米时,求t;
(3)若存在实数t1 , t2(t1≠t2)当t=t1或t2时,足球距离地面的高度都为m(米),求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
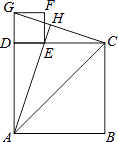
(1)求sin∠EAC的值.
(2)求线段AH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y1=ax2+bx,y2=ax+b(ab≠0).在同一平面直角坐标系中.
(1)若函数y1的图象过点(﹣1,0),函数y2的图象过点(1,2),求a,b的值.
(2)若函数y2的图象经过y1的顶点.
①求证:2a+b=0;
②当1<x< 时,比较y1 , y2的大小.
时,比较y1 , y2的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ,求AQ的长.
,求AQ的长. -
科目: 来源: 题型:
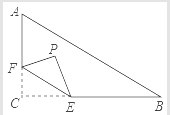
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,若点P能落在线段AB上,则线段CF长的最小值是_____.
相关试题

