【题目】模型建立:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.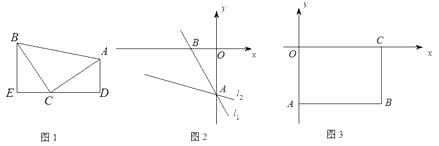
(1)求证:△BEC≌△CDA;
(2)模型应用:
①已知直线l1:y=- ![]() x-4与y轴交于A点,将直线l1绕着A点逆时针旋转45°至l2 , 如图2,求l2的函数解析式;
x-4与y轴交于A点,将直线l1绕着A点逆时针旋转45°至l2 , 如图2,求l2的函数解析式;
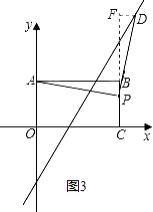
②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,-6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第四象限,且是直线y=-2x+6上的一点,若△APD是不以点A为直角顶点的等腰Rt△,请求出点D的坐标.
参考答案:
【答案】
(1)证明:∵△ABC为等腰直角三角形,∴CB=CA,又∵AD⊥CD,BE⊥EC,∴∠D=∠E=90°,∠ACD+∠BCE=180°-90°=90°,又∵∠EBC+∠BCE=90°,∴∠ACD=∠EBC,在△ACD与△CBE中, 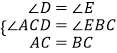 ,∴△ACD≌△EBC(AAS)
,∴△ACD≌△EBC(AAS)
(2)解:①如图1,过点B作BC⊥AB于点B,交l2于点C,过C作CD⊥x轴于D,
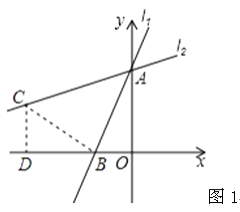
∵∠BAC=45°,∴△ABC为等腰Rt△,由(1)可知:△CBD≌△BAO,∴BD=AO,CD=OB,∵直线l1:y=- ![]() x-4,
x-4, ![]() ∴A(0,-4),B(-3,0),∴BD=AO=4.CD=OB=3,∴OD=4+3=7,∴C(-7,-3),设l2的解析式为y=kx+b(k≠0),∴
∴A(0,-4),B(-3,0),∴BD=AO=4.CD=OB=3,∴OD=4+3=7,∴C(-7,-3),设l2的解析式为y=kx+b(k≠0),∴ ![]() ∴
∴ 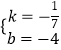 .
.
∴l2的解析式:y=- ![]() x-4.
x-4.
②当点D位于直线y=2x-6上时,分三种情况:如图2,
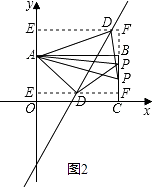
1)点D为直角顶点,分两种情况:当点D在矩形AOCB的内部时,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,设D(x,2x-6);则OE=2x-6,AE=6-(2x-6)=12-2x,DF=EF-DE=8-x;则△ADE≌△DPF,得DF=AE,即:12-2x=8-x,x=4;∴D(4,2);
当点D在矩形AOCB的外部时,设D(x,2x-6);则OE=2x-6,AE=OE-OA=2x-6-6=2x-12,DF=EF-DE=8-x;
同1可知:△ADE≌△DPF,∴AE=DF,即:2x-12=8-x, x= ![]() ,∴D(
,∴D( ![]() )
)
2)点P为直角顶点,显然此时点D位于矩形AOCB的外部;设点D(x,2x-6),则CF=2x-6,BF=2x-6-6=2x-12;
同(1)可得,△APB≌△BDF,∴AB=PF=8,PB=DF=x-8;∴BF=PF-PB=8-(x-8)=16-x;联立两个表示BF的式子可得:2x-12=16-x,即x= ![]() ,∴D(
,∴D( ![]() ).
).
综上所述,点D坐标为(4,-2)或( ![]() )或(
)或( ![]() ).
).
【解析】(1)先根据△ABC为等腰直角三角形得出CB=CA,再由AAS定理可知△ACD≌△CBE;
(2)①过点B作BC⊥AB于点B,交l2于点C,过C作CD⊥x轴于D,根据∠BAC=45°可知△ABC为等腰Rt△,由(1)可知△CBD≌△BAO,由全等三角形的性质得出C点坐标,利用待定系数法求出直线l2的函数解析式即可;②分两种情况考虑:如图2所示,1))点D为直角顶点,分两种情况:当点D在矩形AOCB的内部时,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,设D(x,2x-6);则OE=2x-6,AE=6-(2x-6)=12-2x,DF=EF-DE=8-x,利用三角形全等得到DF=AE,即:12-2x=8-x,得x=4,易得D点坐标;当点D在矩形AOCB的外部时,设D(x,2x-6);则OE=2x-6,AE=OE-OA=2x-6-6=2x-12,DF=EF-DE=8-x;同1可知:△ADE≌△DPF,AE=DF,即:2x-12=8-x, x= ![]() ,易得D点的坐标;2)点P为直角顶点,显然此时点D位于矩形AOCB的外部如图3所示,设点D(x,2x-6),则CF=2x-6,BF=2x-6-6=2x-12;同(1)可得,△APB≌△BDF,利用三角形全等可得AB=PF=8,PB=DF=x-8;故BF=PF-PB=8-(x-8)=16-x,即可确定出D点坐标。
,易得D点的坐标;2)点P为直角顶点,显然此时点D位于矩形AOCB的外部如图3所示,设点D(x,2x-6),则CF=2x-6,BF=2x-6-6=2x-12;同(1)可得,△APB≌△BDF,利用三角形全等可得AB=PF=8,PB=DF=x-8;故BF=PF-PB=8-(x-8)=16-x,即可确定出D点坐标。
【考点精析】本题主要考查了等腰直角三角形和确定一次函数的表达式的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(x,y)在第二象限,且到x轴的距离是2,到y轴的距离是3,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的边长为4厘米,E为AD边的中点,F为AB边上一点,动点P从点B出发,沿B→C→D→E,向终点E以每秒a厘米的速度运动,设运动时间为t秒,△PBF的面积记为S. S与t的部分函数图象如图2所示,已知点M(1,
 )、N(5,6)在S与t的函数图象上.
)、N(5,6)在S与t的函数图象上.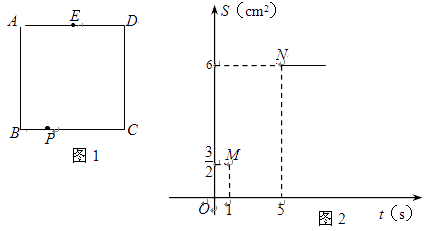
(1)求线段BF的长及a的值;
(2)写出S与t的函数关系式,并补全该函数图象;
(3)当t为多少时,△PBF的面积S为4. -
科目: 来源: 题型:
查看答案和解析>>【题目】假如你想知道你们班同学的身高情况,你必须进行调查,然后对你的调查结果加以总结,那么:
(1)你调查的问题是 ;
(2)你调查的对象是;
(3)你感兴趣的是调查对象的 ;
(4)你的调查方式是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某采摘农场计划种植A,B两种草莓共6亩,根据表格信息,解答下列问题:
项目 品种
A
B
年亩产(单位:千克)
1200
2000
采摘价格
(单位:元/千克)
60
40
(1)若该农场每年草莓全部被采摘的总收入为460000元,那么A、B两种草莓各种多少亩?
(2)若要求种植A种草莓的亩数不少于种植B种草莓的一半,那么种植A种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?并求出最多总收入.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市商店为了对某种商品促销,将定价为3元的商品,以下列方式优惠销售:若购买不超过5件,按原价付款;若一次性购买5件以上,超过部分打八折.如果用27元钱,最多可以购买该商品( )件
A. 9B. 10C. 11D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下列人数次数分布表,回答下列问题:
次数x
人数
60≤x<80
2
80≤x<100
5
100≤x<120
21
120≤x<140
13
140≤x<160
8
160≤x<180
4
(1)全班有多少人?
(2)组距、组数是多少?
(3)跳绳次数在100≤x<140范围内同学有多少人,占全班的百分之几(精确到0.01%)?
相关试题

