搜索
【题目】如图，将△MNP的三边分别向两边延长，并在每两条延长线上任取两点连接起来，又得到了三个新的三角形．求证：∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝360°.
参考答案：
【答案】详见解析
【解析】
利用三角形外角的性质，把∠A+∠B转化为∠1，∠C＋∠D转化为∠2，∠E＋∠F转化为∠3，继续利用外角性质，把∠1＋∠2＋∠3转化为两倍三角形的内角和即可得证。
证明：如图
∵∠1＝∠A＋∠B，∠2＝∠C＋∠D，∠3＝∠E＋∠F，
∴∠1＋∠2＋∠3＝∠A＋∠B＋∠C＋∠D＋∠E＋∠F.
又∵∠1＝∠4＋∠5，∠2＝∠4＋∠6，∠3＝∠5＋∠6，
∴∠1＋∠2＋∠3＝∠4＋∠5＋∠4＋∠6＋∠5＋∠6
＝2(∠4＋∠5＋∠6)
＝2×180°＝360°，
∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝360°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等腰直角三角形ABC位于第一象限，AB=AC=2，直角顶点A在直线y=x上，其中A点的横坐标为1，且两条直角边AB、AC分别平行于x轴、y轴，若双曲线
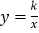(k≠0)与△ABC有交点，则k的取值范围是（ ）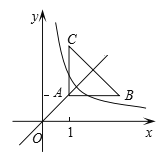
A. 1≤k≤4 B. 1≤k＜4 C. 1＜k＜2 D. 1≤k≤3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，两个大小一样的直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB＝10，DH＝4，平移距离为6，则阴影部分面积是_____
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
是由
经过平移得到的，其中A，B，C三点的对应点分别是
，
，
，它们在平面直角坐标系中的坐标如下表所示：
（1）观察表中各对应点坐标的变化，并填空：
__________，
__________．（2）在下图的平面直角坐标系中画出
和．（3）写出
是怎样平移得到的？
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据下图，完成下列推理过程．
(1)∵∠1＝∠A(已知)， ∴AD∥BC
.(________________________________________________________)
(2)∵∠3＝∠4(已知)，∴CD∥AB
.(________________________________________________________)
(3)∵∠2＝∠5(已知)，∴AD∥BC
.(________________________________________________________)
(4)∵∠ADC＋∠C＝180°(已知)，∴AD∥BC
.(________________________________________________________)
-
科目： 来源： 题型：
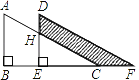
查看答案和解析>>【题目】为了迎接2018年高中招生考试，某中学对全校九年级进行了一次数学摸底考试，并随机抽取了部分学生的测试成绩作为样本进行分析，绘制成如下两幅不完整的统计图1和图2，请你根据图中所给的信息解答下列问题。
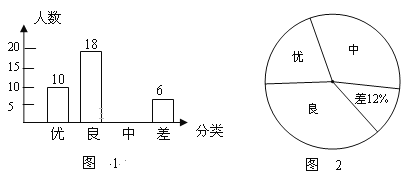
（1）请将表示成绩类别为“中”的条形统计图补充完整；
（2）在扇形统计图中表示成绩为“优”的扇形所对的圆心角为 度；
（3）学校九年级共有600人参加这次数学考试，估计该校有多少名学生成绩可以达到优.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，已知AD∥BC，∠B=∠D=120°．
（1）请问：AB与CD平行吗？为什么？
（2）若点E、F在线段CD上，且满足AC平分∠BAE，AF平分∠DAE，如图②，求∠FAC的度数．
（3）若点E在直线CD上，且满足∠EAC=
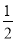∠BAC，求∠ACD：∠AED的值（请自己画出正确图形，并解答）．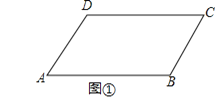
相关试题
