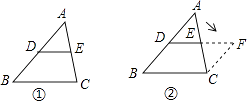【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:
课本研究三角形中位线性质的方法 |

请你利用小亮的发现解决下列问题:
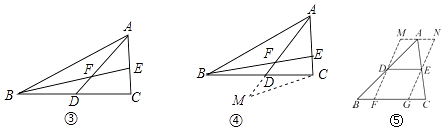
(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.
请你帮助小亮写出辅助线作法并完成论证过程:
(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是 .
参考答案:
【答案】
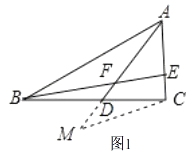
(1)证明:如图1,延长AD至点M,使MD=FD,连接MC,
在△BDF和△CDM中,BD=CD,∠BDF=∠CDM,DF=DM.
∴△BDF≌△CDM(SAS).
∴MC=BF,∠M=∠BFM.
∵EA=EF,
∴∠EAF=∠EFA.
∵∠AFE=∠BFM,
∴∠M=∠MAC.
∴AC=MC.
∴BF=AC.
(2)8+10 ![]()
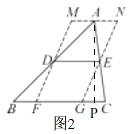
【解析】(2)如图2,
在△ABC中,∠B=45°,AB=10,BC=8,
∵DE是△ABC的中位线.
∴DE= ![]() BC=4,DE∥BC
BC=4,DE∥BC
∵DF∥EG,MN∥BC,
∴四边形DEGF,DENM,FGNM是平行四边形,
∴MN=FG=DE=4,
∴要四边形MFGN周长的最小只有MF=NG最小,
即:MF⊥BC,
∴平行四边形FGNM是矩形,
过点A作AP⊥BC于P,
∴AP=MF=NG,
在Rt△ABP中,∠B=45°,AB=10,
∴AP=5 ![]() ,
,
∴MF=NG=5 ![]() ,
,
即四边形MFGN周长的最小值是8+10 ![]() .
.
所以答案是:8+10 ![]() .
.
【考点精析】利用三角形中位线定理对题目进行判断即可得到答案,需要熟知连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了丰富学生课余生活,决定开设以下体育课外活动项目:A.版画 B.保龄球C.航模 D.园艺种植,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:

(1)这次被调查的学生共有人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的保龄球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加保龄球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答) -
科目: 来源: 题型:
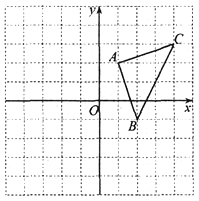
查看答案和解析>>【题目】如图,平面直角坐标系中,△ABC的顶点坐标为:A(1,2),B(2, 一1), C (4, 3).
(1)将△ABC向左平移2个单位长度,再向上平移1个单位长度,得△A'B'C'.画出△A'B'C',并写出△A'B'C'的顶点坐标;
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
根据城市规划设计,某市工程队准备为该城市修建一条长4800米的公路.铺设600m后,为了尽量减少施工对城市交通造成的影响,该工程队增加人力,实际每天修建公路的长度是原计划的2倍,结果9天完成任务,该工程队原计划每天铺设公路多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×3.142﹣4×3.14×3.28+3.282”,他觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
x=﹣1,y=1
x=1,y=0
x=3,y=2
x=1,y=1
x=5,y=3
A=2x﹣y
﹣3
2
4
1
7
B=4x2﹣4xy+y2
9
4
(2)观察表格,你发现A与B有什么关系?
解决问题:
(3)请结合上述的有关信息,计算4×3.142﹣4×3.14×3.28+3.282.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画出函数y=2x+4的图像,并结合图像解决下列问题:
(1)写出方程2x+4=0的解;
(2)当﹣4≤y时,求相应x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点A、点B的坐标分别为(4,0)、(0,3).
(1)求AB的长度.
(2)如图2,若以AB为边在第一象限内作正方形ABCD,求点C的坐标.

(3)在x轴上是否存一点P,使得⊿ABP是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
相关试题