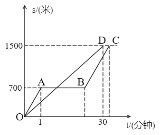
【题目】“龟兔赛跑”的故事同学们都听过,图中的线段OD和折线OABC表示龟兔赛跑时路程与时间的关系,请根据图中的信息,解决下列问题:
(1)填空:折线OABC表示赛跑过程中_________(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全程是_______米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后以400米/分钟的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少时间?
参考答案:
【答案】(1) 兔子,1500;(2) 700,50;(3) 14;(4) 27.5.
【解析】
(1)兔子在赛跑途中有停留,故折线表示兔子的,直线表示乌龟的;
(2)兔子在起初对应的是线段OA,其运动时间是1分钟,运动路程是700米,路程除时间即为速度;乌龟一直匀速,对应的是OD段,其路程是1500米,时间是30分钟,由此可算出速度;
(3)用700除以(2)中算出的乌龟的速度,即得到乌龟追上兔子所用的时间;
(4)兔子醒来后对应的是线段BC,算出BC段所用的时间,再加上OA段时间,加上睡觉时间,再加上0.5分钟等于乌龟时间即可求解.
解:(1)∵乌龟是一直跑的而兔子中间由休息的时刻,
∴折线OABC表示赛跑过程中兔子的路程与时间的关系;
由图像可知,赛跑的全过程为1500米.
故答案为:兔子,1500.
(2)结合图像可知:
兔子在起初每分钟跑700÷1=700(米)
乌龟每分钟爬1500÷30=50(米)
故答案为:700,50.
(3)700÷50=14分钟
∴乌龟用了14分钟追上了正在睡觉的兔子.
故答案为:14.
(4)最开始兔子跑700米,用了1分钟
最后兔子开始追,用了(1500-700)÷400=2分钟
乌龟爬完整个路程用了30分钟,
设兔子中间睡觉的时间为t分钟,由题意得:
1+t+2=30+0.5
解得t=27.5分钟,故兔子中间休息了27.5分钟.
故答案为:27.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,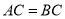 ,若有一动点
,若有一动点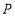 从
从 出发,沿
出发,沿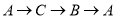 匀速运动,则
匀速运动,则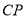 的长度
的长度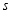 与时间
与时间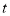 之间的关系用图像表示大致是( )
之间的关系用图像表示大致是( )
A.
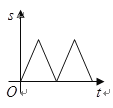 B.
B.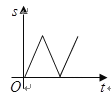
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)
 +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;(2)如果(2+
 )a-(1-
)a-(1- )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值. -
科目: 来源: 题型:
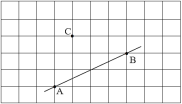
查看答案和解析>>【题目】(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线__________的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段__________最短,理由:______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣4
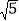 x+12+m=0.
x+12+m=0.(1)若方程的一个根是
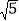 ,求m的值及方程的另一根;
,求m的值及方程的另一根;(2)若方程的两根恰为等腰三角形的两腰,而这个三角形的底边为m,求m的值及这个等腰三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若x,y都是实数,且y=
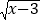 +
+ +8,求5x+13y+6的值;
+8,求5x+13y+6的值;(2)已知△ABC的三边长分别为a,b,c,且满足
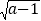 +b2-6b+9=0,求c的取值范围。
+b2-6b+9=0,求c的取值范围。 -
科目: 来源: 题型:
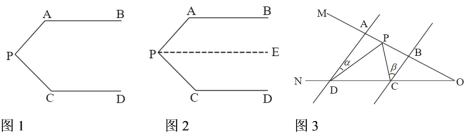
查看答案和解析>>【题目】(1)同题情景:如图1,AB//CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明想到一种方法,但是没有解答完:
如图2,过P作PE//AB,∴∠APE+∠PAB=180°,
∴∠APE=180°-∠PAB=180°-130°=50°
∵AB//CD,∴PE//CD.
……
请你帮助小明完成剩余的解答.
(2)问题迁移:请你依据小明的解题思路,解答下面的问题:
如图3,AD//BC,当点P在A、B两点之间时,∠ADP=∠α,∠BCP=∠β,则∠CPD,∠α,∠β之间有何数量关系?请说明理由.
相关试题

