【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.

参考答案:
【答案】135
【解析】试题分析:根据“爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°”可以求出AD的长,然后根据“在一楼房的底端A点处观测观光塔顶端C处的仰角是60°”可以求出CD的长.
解:∵爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,
tan30°=![]() ,
,
解得,![]() =
=![]() ,
,
∴AD=45![]() ,
,
∵在一楼房的底端A点处观测观光塔顶端C处的仰角是60°,
∴在Rt△ACD中,
CD=ADtan60°=45![]() ×
×![]() =135米.
=135米.
故答案为135米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于数据:80,88,85,85,83,83,84.下列说法中错误的有( )
A、这组数据的平均数是84;
B、这组数据的众数是85;
C、这组数据的中位数是84;
D、这组数据的方差是36.
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
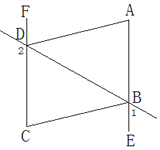
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)求证:BC平分∠DBE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,动点C在⊙O的弦AB上运动,AB=
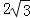 ,连接OC,CD⊥OC交⊙O于点D.则CD的最大值为 .
,连接OC,CD⊥OC交⊙O于点D.则CD的最大值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点 A、B,M均在数轴上,点M对应的数为,点A与点M的距离为3,点A与点B的距离为6,则点B到数轴原点O的距离为 ________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】5m﹣m﹣8m=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”.如果等腰三角形的“内角正度值”为45°,那么该等腰三角形的顶角等于_________。
相关试题

