搜索
【题目】如图，已知AB、CD、EF相交于O点，AB⊥CD，
（1）写出∠AOF, ∠DOE的邻补角；
（2）写出∠AOE, ∠DOF的对顶角；
(3)如果∠DOF＝38°求∠AOF和∠AOE的度数
参考答案：
【答案】（1）∠BOF或∠AOE；∠DOF或∠COE；（2）∠BOF；∠COE；(3)52°，128°.
【解析】
（1）根据邻补角的定义即可求解.
（2）根据对顶角的定义即可求解.
（3）根据垂直的定义得到
即可求出
的度数，根据邻补角的定义即可求出∠AOE的度数.
（1）∠AOF的邻补角是∠BOF或∠AOE, ∠DOE的邻补角是∠DOF或∠COE；
（2）∠AOE的对顶角是∠BOF, ∠DOF的对顶角是∠COE；
（3）
AB⊥CD，
∠DOF=38°,
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系中，长方形
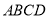的三个顶点的坐标为
，
，
，且
轴，点
是长方形内一点（不含边界）.
（1）求
，
的取值范围.（2）若将点
向左移动8个单位，再向上移动2个单位到点
，若点恰好与点
关于
轴对称，求，的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立．
（1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．
（2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．
①求证：BD⊥CF；
②当AB=4，AD=
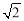时，求线段BG的长．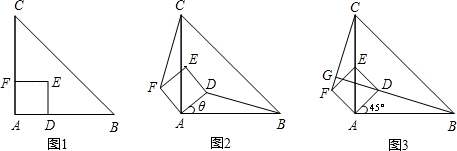
-
科目： 来源： 题型：
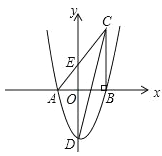
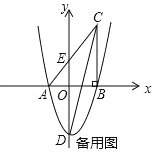
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC 的一边 AB 在 x 轴上，∠ABC=90°，点 C（4，8） 在第一象限内，AC 与 y 轴交于点 E，抛物线 y=
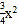+bx+c 经过 A、B 两点，与 y 轴交于点 D（0，﹣6）．（1）请直接写出抛物线的表达式；
（2）求 ED 的长；
（3）若点 M 是 x 轴上一点（不与点 A 重合），抛物线上是否存在点 N，使∠CAN=∠MAN．若存在，请直接写出点 N 的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】十八大报告首次提出建设生态文明，建设美丽中国. 十九大报告再次明确，到2035年美丽中国目标基本实现.森林是人类生存发展的重要生态保障，提高森林的数量和质量对生态文明建设非常关键 .截止到2013年，我国已经进行了八次森林资源清查，其中全国和北京的森林面积和森林覆盖率情况如下：
表1 全国森林面积和森林覆盖率
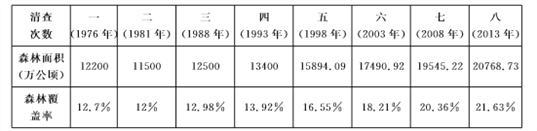
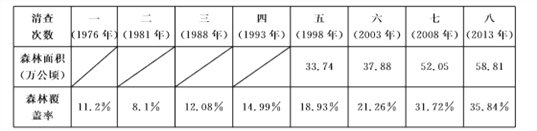
表2 北京森林面积和森林覆盖率
（以上数据来源于中国林业网）
请根据以上信息解答下列问题：
(1)从第________次清查开始，北京的森林覆盖率超过全国的森林覆盖率；
(2)补全以下北京森林覆盖率折线统计图，并在图中标明相应数据；
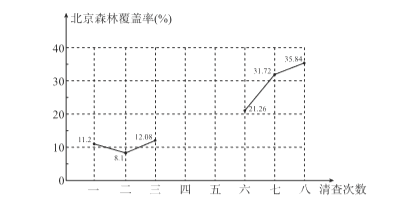
(3) 第八次清查的全国森林面积20768.73（万公顷）记为a，全国森林覆盖率21.63%记为b，到2018年第九次森林资源清查时，如果全国森林覆盖率达到27.15%，那么全国森林面积可以达到________万公顷（用含a和b的式子表示）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是一个汉字“互”字，其中，AB∥CD，∠1=∠2，∠MGH=∠MEF.
求证：∠MEF=∠GHN.
证明：∵ AB∥CD（已知）
∴∠1=∠3（ ）
又∵∠1=∠2（已知）
∴∠2=∠3（ ）
∴ME∥HN （ ）
∴∠MGH=∠ ( )( )
又∵∠MGH=∠MEF (已知)
∴∠MEF=∠GHN（ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校八年级两个班，各选派10名学生参加学校举行的“建模”大赛预赛，各参赛选手的成绩如下：
八（1）班：88，91，92，93，93，93，94，98，98，100；
八（2）班：89，93，93，93，95，96，96，98，98，99.
通过整理，得到数据分析表如下：
班级
最高分
平均分
中位数
众数
方差
八（1）班
100
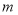
93
93
12
八（2）班
99
95
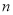
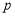
8.4
（1）直接写出表中
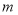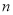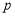、、的值为：
_____，
_____，
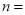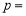_____；（2）依据数据分析表，有人说：“最高分在（1）班，（1）班的成绩比（2）班好.”但也有人说（2）班的成绩要好.请给出两条支持八（2）班成绩好的理由；
（3）学校从平均数、中位数、众数、方差中选取确定了一个成绩，等于或大于这个成绩的学生被评定为“优秀”等级，如果八（2）班有一半的学生能够达到“优秀”等级，认为这个成绩应定为_____分.
相关试题
