【题目】如图是二次函数![]() 图象的一部分,其对称轴是
图象的一部分,其对称轴是![]() ,且过点
,且过点![]() ,下列说法:①
,下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中说法正确的是( )
,其中说法正确的是( )

A. ①② B. ②③
C. ①②④ D. ②③④
参考答案:
【答案】A
【解析】试题解析:∵二次函数的图象的开口向上,
∴a>0,
∵二次函数的图象y轴的交点在y轴的负半轴上,
∴c<0,
∵二次函数图象的对称轴是直线x=1,
![]() ∴b=2a>0,
∴b=2a>0,
∴abc<0,∴①正确;
2ab=2a2a=0,∴②正确;
∵二次函数![]() 图象的一部分,其对称轴为x=1,且过点(3,0).
图象的一部分,其对称轴为x=1,且过点(3,0).
∴与x轴的另一个交点的坐标是(1,0),
∴把x=2代入![]() 得:y=4a+2b+c>0,∴③错误;
得:y=4a+2b+c>0,∴③错误;
∵二次函数![]() 图象的对称轴为x=1,
图象的对称轴为x=1,
∴点(5,y1)关于对称轴的对称点的坐标是(3,y1),
根据当x>1时,y随x的增大而增大,
![]()
![]() ∴④错误;
∴④错误;
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 的图象交
的图象交 轴于
轴于 两点,交
两点,交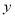 轴于点
轴于点 ,点
,点 的坐标为
的坐标为 ,顶点
,顶点 的坐标为
的坐标为 .
.
(1)求二次函数的解析式和直线
 的解析式;
的解析式;(2)点
 是直线
是直线 上的一个动点,过点
上的一个动点,过点 作
作 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点 ,当点
,当点 在第一象限时,求线段
在第一象限时,求线段 长度的最大值;
长度的最大值;(3)在抛物线上是否存在异于
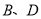 的点
的点 ,使
,使 中
中 边上的高为
边上的高为 ,若存在求出点
,若存在求出点 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.

(1)求点B及点D的坐标.
(2)连结BD,CD,抛物线的对称轴与x轴交于点E.
①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)-5+6-7+8
(2)
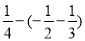
(3)10-1÷(
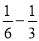 )÷
)÷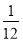

(4)
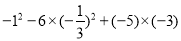
(5)
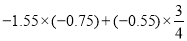
(6)
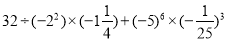
-
科目: 来源: 题型:
查看答案和解析>>【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线
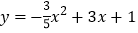 的一部分,如图
的一部分,如图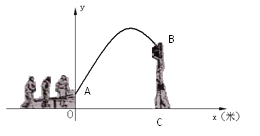
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
-
科目: 来源: 题型:
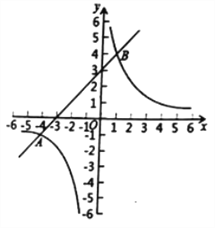
查看答案和解析>>【题目】(9分)已知:如图,在平面直角坐标系
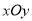 中,反比例函数
中,反比例函数 的图象与一次函数
的图象与一次函数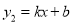 的图象交于点
的图象交于点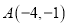 和点和
和点和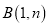 .
.
(1)求这两个函数的表达式;
(2)观察图象,当
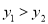 时,直接写出自变量
时,直接写出自变量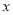 的取值范围;
的取值范围;(3)求
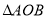 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
解方程:x4﹣6x2+5=0.这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2﹣6y+5=0…①,
解这个方程得:y1=1,y2=5.
当y=1时,x2=1,∴x=±1;
当y=5时,x2=5,∴x=±
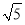
所以原方程有四个根:x1=1,x2=﹣1,x3=
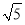 ,x4=﹣
,x4=﹣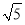 .
.在这个过程中,我们利用换元法达到降次的目的,体现了转化的数学思想.
(1)解方程(x2﹣x)2﹣4(x2﹣x)﹣12=0时,若设y=x2﹣x,则原方程可转化为 ;求出x
(2)利用换元法解方程:
 =2.
=2.
相关试题

