【题目】如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.
(1)求∠EDG的度数.
(2)如图2,E为BC的中点,连接BF.
①求证:BF∥DE;
②若正方形边长为12,求线段AG的长.


参考答案:
【答案】(1)45°;(2)①用外角证明平行见解析,②4
【解析】整体分析:
(1)判断DE,DG分别平分∠CDF,∠ADF;(2)①由ED平分∠CEG,EF=EB,结合三角形的一个外角等于和它不相邻的两个内角的和得到∠CED=∠EBF;(3)由(1)中的结论,在Rt△BEG中用勾股定理列方程求解.
(1)解:由折叠知,DF=DC,∠CDE=∠FDE,∠DFE=∠DCE=90°,
∵AD=CD,所以AD=DF,
∵∠DAG=90°,DG=DG,
∴△DAG≌△DFG,∴∠ADG=∠FDG,
∴∠EDG=∠EDF+∠FDG=![]() (∠CDF+∠FDA)=
(∠CDF+∠FDA)=![]() ×90°=45°.
×90°=45°.
(2)①证明:由折叠知,CE=EF,∠CED=∠FED,
∵E为BC的中点,∴BE=CE,∴EF=BE,
∴∠EBF=∠EFB,
∵∠CEG=∠EBF+∠EFB,∴∠CED=∠EBF,
∴BF∥DE.
(3)由(1)得EC=EF,GA=GF,
∴EG=EC+GA.
设AG=x,则BG=12-x,
又EB=EC=EF=6,
在Rt△BEG中,由勾股定理得:BG2+BE2=EG2.
∴(12-x)2+62=(x+6)2,解得x=4.
所以线段AG的长为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)2xy-
 (4xy-8x2y2)+2(3xy-5x2y2),其中x=
(4xy-8x2y2)+2(3xy-5x2y2),其中x= ,y=-3.
,y=-3.(2)-a2b+(3ab2-a2b)-2(2ab2-a2b),其中a=1,b=-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是关于x的二次函数,求:
是关于x的二次函数,求:
(1)满足条件的k的值;
(2)当k为何值时,抛物线有最高点?求出这个最高点;
(3)当k为何值时,函数有最小值?最小值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD的对角线AC、BD交于点O,若OE=OF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)求证:四边形DEBF是平行四边形;
(3)若OD=OE=OF,则四边形DEBF是什么特殊的四边形,请证明.
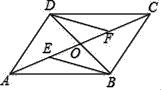
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列哪组条件能够判别四边形ABCD是平行四边形?( )

A. AB∥CD,AD=BC B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D D. AB=AD,CB=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
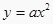 与直线
与直线 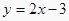 交于点P(1,b).
交于点P(1,b).
(1)求a、b的值;
(2)写出二次函数的关系式,并指出x取何值时,该函数的y随x的增大而减小. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( ).
A. m=-2是方程m-2=0的解 B. m=6是方程3m+18=0的解
C. x=-1是方程-
 =0的解 D. x=
=0的解 D. x=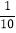 是方程10x=1的解
是方程10x=1的解
相关试题

