【题目】如图是我国某海域内的一个小岛，其平面图如图甲所示，小明据此构造出该岛的一个数学模型如图乙所示，其中∠B＝∠D＝90°，AB＝BC＝15千米，CD＝3千米，请据此解答如下问题：

(1)求该岛的周长和面积；(结果保留整数，参考数据：≈1.414，≈1.732，≈2.449)

(2)求∠ACD的余弦值．

参考答案：

【答案】(1) 周长:55千米，面积:157平方千米;(2).

【解析】

（1）连接AC，根据AB=BC=15千米，∠B=90°得到∠BAC=∠ACB=45° ，AC=15千米，再根据∠D=90°利用勾股定理求得AD的长后即可求周长和面积；

（2）直接利用余弦的定义求解即可

（1）连接AC

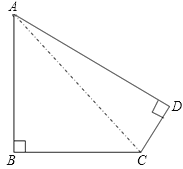
∵AB=BC=15千米，∠B=90°

∴∠BAC=∠ACB=45° AC=15千米

又∵∠D=90°

∴AD=（千米）

∴周长=AB+BC+CD+DA=30+3+12=30+4.242+20.784≈55（千米）

面积=S△ABC+S△ADC=112.5+18≈157（平方千米）

（2）cos∠ACD=.

关闭