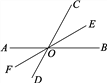
【题目】如图,直线AB、CD相交于点O,OE平分∠BOC,∠BOC=70°,OF是OE的反向延长线.
(1)求∠DOF与∠BOF的度数;
(2)OF平分∠AOD吗?为什么?
参考答案:
【答案】(1)∠DOF=35°,∠BOF=145° (2)OF平分∠AOD.
【解析】试题分析:(1)根据角平分线的定义,可求得∠BOE=∠COE==35°,再根据对顶角的性质及邻补角的定义即可求得∠DOF与∠BOF的度数;
(2)根据OF分∠AOD的两部分角的度数即可说明.
试题解析:(1)∵OE平分∠BOC,
∴∠BOE=∠COE=![]() ∠BOC=
∠BOC=![]() ×70°=35°,
×70°=35°,
∴∠DOF=∠COE=35°,∠BOF=180°-∠BOE=180°-35°=145°;
(2)OF平分∠AOD,理由:
∵∠AOD=∠BOE=35°,∠DOF=35°,
∴∠AOF=∠DOF, 即OF平分∠AOD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴的正半轴上,OA=4,AB=5,点D在反比例函数
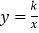 (k>0)的图象上,
(k>0)的图象上,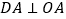 ,点P在y轴负半轴上,OP=7.
,点P在y轴负半轴上,OP=7.(1)求点B的坐标和线段PB的长;
(2)当
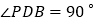 时,求反比例函数的解析式。
时,求反比例函数的解析式。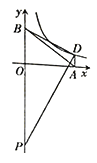
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
若x满足(x-2015)(2002-x)=-302,试求(x-2015)2+(2002-x)2的值.
解:设x-2015=a,2002-x=b,则ab=-302且a+b=(x-2015)+(2002-x)=-13.
∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2-2ab=(-13)2-2×(-302)=773,即(x-2015)2+(2002-x)2的值为773.
解决问题:
请你根据上述材料的解题思路,完成下面一题的解答过程,若y满足(y-2015)2+(y-2016)2=4035,试求(y-2015)(y-2016)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果﹣3m表示一个物体向北运动3m,那么+4m表示______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形操场的长是宽的2.5倍,根据需要将它扩建,把它的长和宽各加长20m后,它的长是宽的2倍,求扩建前长方形操场的周长是______m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织网络安全知识竞赛活动,其中七年级6个班组每班参赛人数相同,学校对该年级的获奖人数进行统计,得到每班平均获奖15人,并制作成如图所示不完整的折线统计图.
(1)请将折线统计图补充完整,并直接写出该年级获奖人数最多的班级是 班;
(2)若二班获奖人数占班级参赛人数的32%,则全年级参赛人数是 人;
(3)若该年级并列第一名有男、女同学各2名,从中随机选取2名参加市级比赛,请用列表或画树状图的方法求出恰好选中一男一女的概率。
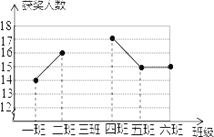
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3a+2a=5a2
B.a6÷a2=a3
C.(﹣3a3)2=9a6
D.(a+2)2=a2+4
相关试题

