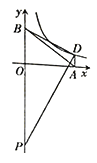
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴的正半轴上,OA=4,AB=5,点D在反比例函数![]() (k>0)的图象上,
(k>0)的图象上,![]() ,点P在y轴负半轴上,OP=7.
,点P在y轴负半轴上,OP=7.
(1)求点B的坐标和线段PB的长;
(2)当![]() 时,求反比例函数的解析式。
时,求反比例函数的解析式。
参考答案:
【答案】(1)10(2)![]()
【解析】试题分析:(1)根据勾股定理求出OB,即可得出答案;(2)设D的坐标是(4,y),证△BDM∽△DPM,得出比例式,代入即可求出y,把D的坐标代入求出即可.
试题解析:(1)∵AB=5,OA=4,∠AOB=90°,
∴由勾股定理得:OB=3,即点B的坐标是(0,3).
∵OP=7,
∴线段PB=OB+OP=3+7=10.
(2)过点D作DM⊥y轴于M,

∵∠PDB=90°,
∴∠BDP=∠DMB=∠DMP=90°
∴∠DBM+∠BDM=90°,∠BDM+∠MDP=90°
∴∠DBM=∠MDP
∴△DBM∽△PDM
∴![]()
∵OA=4,DM⊥y轴,设D点的坐标为(4,y)(y>0),
∴![]() ,
,
解得y=1(y=-5舍去),
即点D的坐标为(4,1)
把点D的坐标代入![]() ,得k=4,即反比例函数的解析式是
,得k=4,即反比例函数的解析式是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校初三年级开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,如果购买3张两人学习桌,1张三人学习桌需220元;如果购买2张两人学习桌,3张三人学习桌需310元.
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过6000元,购买两种学习桌共98张,以至少满足248名学生的需求,设购买两人学习桌x张,购买两人学习桌和三人学习桌的总费用为W 元,求出W与x的函数关系式;求出所有的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】43°29′+36°31′=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4ax2﹣ay2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
若x满足(x-2015)(2002-x)=-302,试求(x-2015)2+(2002-x)2的值.
解:设x-2015=a,2002-x=b,则ab=-302且a+b=(x-2015)+(2002-x)=-13.
∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2-2ab=(-13)2-2×(-302)=773,即(x-2015)2+(2002-x)2的值为773.
解决问题:
请你根据上述材料的解题思路,完成下面一题的解答过程,若y满足(y-2015)2+(y-2016)2=4035,试求(y-2015)(y-2016)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果﹣3m表示一个物体向北运动3m,那么+4m表示______.
-
科目: 来源: 题型:
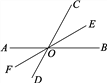
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOC,∠BOC=70°,OF是OE的反向延长线.
(1)求∠DOF与∠BOF的度数;
(2)OF平分∠AOD吗?为什么?
相关试题

