【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.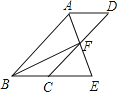
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
参考答案:
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,∴BE=CD
(2)
解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=4,
∵BF⊥AE,
∴AF=EF=2,
∴BF= ![]() =
= ![]() =2
=2 ![]() ,
,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
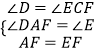 ,
,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积= ![]() AEBF=
AEBF= ![]() ×4×2
×4×2 ![]() =4
=4 ![]() .
.
【解析】(1)由平行四边形的性质和角平分线得出∠BAE=∠BEA,即可得出AB=BE;
(2)先证明△ABE是等边三角形,得出AE=AB=4,AF=EF=2,由勾股定理求出BF,由AAS证明△ADF≌△ECF,得出△ADF的面积=△ECF的面积,因此平行四边形ABCD的面积=△ABE的面积= ![]() AEBF,即可得出结果.此题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定、等边三角形的判定与性质、勾股定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题(2)的关键.
AEBF,即可得出结果.此题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定、等边三角形的判定与性质、勾股定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题(2)的关键.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等.经洽谈,甲商场的优惠方案是:每购买10套队服,送1个足球;乙商场的优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)每套队服和每个足球的价格分别是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所需的费用.
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某快递公司有甲、乙、丙三个机器人分配快件,甲单独完成需要x小时,乙单独完成需要y小时,丙单独完成需要z小时.
(1)求甲单独完成的时间是乙丙合作完成时间的几倍?
(2)若甲单独完成的时间是乙丙合作完成时间的a倍,乙单独完成的时间是甲丙合作完成时间的b倍,丙单独完成的时间是甲乙合作完成时间的c倍,求
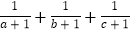 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,点P是它内部一点,OP=2,如果点Q、点R分别是OA、OB上的两个动点,那么PQ+QR+RP的最小值是__________.

-
科目: 来源: 题型:
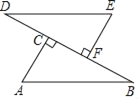
查看答案和解析>>【题目】如图,D、C、F、B四点在一条直线上,AB=DE,AC⊥BD,EF⊥BD,垂足分别为点C、点F,CD=BF.
求证:(1)△ABC≌△EDF;
(2)AB∥DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,B、C 两点把线段 AD 分成 2:5:3 三部分,M 为 AD 的中点,BM=6cm,则 AD 的长为( )
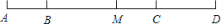
A. 21cm B. 20cm C. 19cm D. 18cm
相关试题

