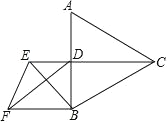
【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.
参考答案:
【答案】![]()
【解析】
首先证明△CBE≌△ABF,推出∠BAF=∠BCE,由CA=CB,CD⊥AB,推出∠BCE=![]() ∠ACB=30°,AD=BD=4,推出∠BAF=30°=定值,根据垂线段最短可知,当DF⊥AF时,DF的值最小.
∠ACB=30°,AD=BD=4,推出∠BAF=30°=定值,根据垂线段最短可知,当DF⊥AF时,DF的值最小.
如图,
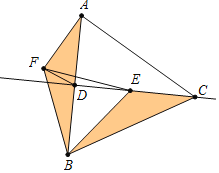
∵△ABC,△BEF的是等边三角形,
∴AB=BC,BF=BE,∠ABC=∠ACB=∠EBF=60°,
∴∠CBE=∠ABF,
在△BCE和△BAF中,
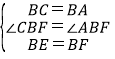 ,
,
∴△CBE≌△ABF(SAS),
∴∠BAF=∠BCE,
∵CA=CB,CD⊥AB,
∴∠BCE=![]() ∠ACB=30°,AD=BD=
∠ACB=30°,AD=BD=![]() ,
,
∴∠BAF=30°是定值,
∴根据垂线段最短可知,当DF⊥AF时,DF的值最小,
∴DF的最小值=![]() AD=
AD=![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是( )
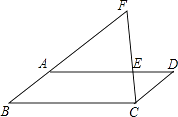
A.EF=2CE
B.S△AEF= S△BCF
S△BCF
C.BF=3CD
D.BC= AE
AE -
科目: 来源: 题型:
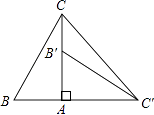
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?
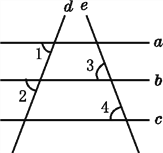
解:a与c平行.
理由:因为∠1=∠2(_________________),
所以a∥b(_________________).
因为∠3=∠4(_________________),
所以b∥c(_________________).
所以a∥c(_________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边三角形ABC的边长为8,P是BC边上一点,连接AP,若AP=7,则BP的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB是⊙O的两条切线,A、B是切点,PA=
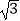 OA,阴影部分的面积为6π,则⊙O的半径长为 .
OA,阴影部分的面积为6π,则⊙O的半径长为 . 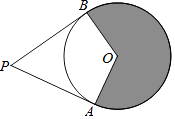
相关试题

