【题目】已知等边三角形ABC的边长为8,P是BC边上一点,连接AP,若AP=7,则BP的长为 .
参考答案:
【答案】3或5
【解析】解:如图1所示, 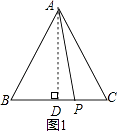
过点A作AD⊥BC,
设DP=x,
∵△ABC为等边三角形,AD⊥BC,
∴BD= ![]() =4,
=4,
在Rt△ABD中,
AD2=AB2﹣BD2=82﹣42=48,
在Rt△APD中,
DP2=AP2﹣AD2=72﹣48=1,
∴DP=1,
∴BP=5;
当点P在AD的左侧时,如图2所示,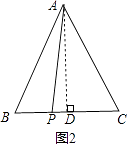
同理可得,BP=BD﹣PD=4﹣1=3,
综上所述,BP的长为3或5,
所以答案是:3或5.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?
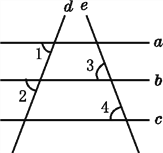
解:a与c平行.
理由:因为∠1=∠2(_________________),
所以a∥b(_________________).
因为∠3=∠4(_________________),
所以b∥c(_________________).
所以a∥c(_________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.
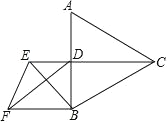
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB是⊙O的两条切线,A、B是切点,PA=
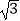 OA,阴影部分的面积为6π,则⊙O的半径长为 .
OA,阴影部分的面积为6π,则⊙O的半径长为 . 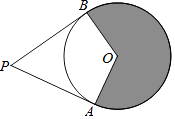
-
科目: 来源: 题型:
查看答案和解析>>【题目】列代数式.
(1)设某数为x,用代数式表示比某数的2倍少1的数;
(2)a,b两数的平方和减去它们的积的2倍;
(3)某工厂第一年生产a件产品,第二年比第一年增产了20%,则两年共生产产品的件数为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值.
(1)(2x2y-4xy2)-(-
 xy2+x2y),其中x=-1,y=2;
xy2+x2y),其中x=-1,y=2;(2)2x2-[3(-
 x2+
x2+ xy)-2y2]-2(x2-xy+2y2),其中x,y满足|x-
xy)-2y2]-2(x2-xy+2y2),其中x,y满足|x- |+(y+1)2=0.
|+(y+1)2=0.
相关试题

