【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE. 
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB= ![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
参考答案:
【答案】
(1)解:直线CE与⊙O相切
理由如下:
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE;
连接OE,则∠DAC=∠AEO=∠DCE;
∵∠DCE+∠DEC=90°
∴∠AE0+∠DEC=90°
∴∠OEC=90°,即OE⊥CE.
又OE是⊙O的半径,
∴直线CE与⊙O相切.
(2)解:∵tan∠ACB= ![]() =
= ![]() ,BC=2,
,BC=2,
∴AB=BCtan∠ACB= ![]() ,
,
∴AC= ![]() ;
;
又∵∠ACB=∠DCE,
∴tan∠DCE=tan∠ACB= ![]() ,
,
∴DE=DCtan∠DCE=1;
方法一:在Rt△CDE中,CE= ![]() =
= ![]() ,
,
连接OE,设⊙O的半径为r,则在Rt△COE中,CO2=OE2+CE2,即 ![]() =r2+3
=r2+3
解得:r= ![]()
方法二:AE=AD﹣DE=1,过点O作OM⊥AE于点M,则AM= ![]() AE=
AE= ![]()
在Rt△AMO中,OA= ![]() =
= ![]() ÷
÷ ![]() =
= ![]()
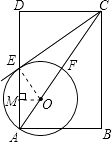
【解析】(1)连接OE.欲证直线CE与⊙O相切,只需证明∠CEO=90°,即OE⊥CE即可;(2)在直角三角形ABC中,根据三角函数的定义可以求得AB= ![]() ,然后根据勾股定理求得AC=
,然后根据勾股定理求得AC= ![]() ,同理知DE=1; 方法一、在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2 , 即
,同理知DE=1; 方法一、在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2 , 即 ![]() =r2+3,从而易得r的值;
=r2+3,从而易得r的值;
方法二、过点O作OM⊥AE于点M,在Rt△AMO中,根据三角函数的定义可以求得r的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC与BD互相垂直,若AB=3,BC=4,CD=5,则AD的长为( )
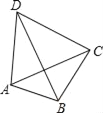
A. 3
 B. 4
B. 4 C. 2
C. 2 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图正方形ABCD边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )
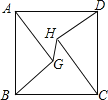
A.
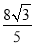 B.
B. 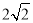 C.
C. 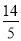 D. 10-5
D. 10-5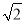
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过原点o和x轴上一点A(4,0),抛物线顶点为E,它的对称轴与x轴交于点D.直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
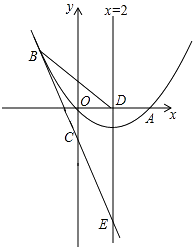
(1)求m的值及该抛物线对应的解析式;
(2)P(x,y)是抛物线上的一点,若S△ADP=S△ADC , 求出所有符合条件的点P的坐标;
(3)点Q是平面内任意一点,点M从点F出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M的运动时间为t秒,是否能使以Q、A、E、M四点为顶点的四边形是菱形.若能,请直接写出点M的运动时间t的值;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,(1)∠BED与∠CBE是直线________,________被直线________所截形成的________角;
(2)∠A与∠CED是直线________,________被直线________所截形成的________角;
(3)∠CBE与∠BEC是直线________,________被直线________所截形成的________角;
(4)∠AEB与∠CBE是直线________,________被直线________所截形成的________角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.今年文学书和科普书的单价与去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
相关试题

