搜索
【题目】如图所示是二次函数y=ax2+bx+c图象的一部分，图象过A点（3，0），二次函数图象对称轴为x=1，给出四个结论：①b2＞4ac；②bc＜0；③2a+b=0；④a+b+c=0，其中正确结论是（ ）
A.②④
B.①③
C.②③
D.①④
参考答案：
【答案】B
【解析】解：①图象与x轴有两个交点，则方程有两个不相等的实数根，b2﹣4ac＞0，b2＞4ac，正确；
②因为开口向下，故a＜0，有﹣ 
＞0，则b＞0，又c＞0，故bc＞0，错误；
③由对称轴x=﹣ =1，得2a+b=0，正确；
④当x=1时，a+b+c＞0，错误；
故①③正确．
故选：B．
将函数图象补全，再进行分析．主要是从抛物线与x轴（y轴）的交点，开口方向，对称轴及x=±1等方面进行判断．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形网格中的△ABC，若小方格边长为1，格点△ABC（顶点是网格线交点的三角形）的顶点A，C的坐标分别为（﹣1，1），（0，﹣2），请你根据所学的知识．
（1）在如图所示的网格平面内作出平面直角坐标系；
（2）作出△ABC关于y轴对称的三角形A1B1C1；
（3）判断△ABC的形状，并求出△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，△ABC顶点的横、纵坐标都是整数．若将△ABC以某点为旋转中心，顺时针旋转90°得到△DEF，则旋转中心的坐标是（ ）
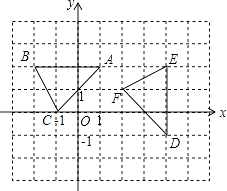
A.（0，0）
B.（1，0）
C.（1，﹣1）
D.（2.5，0.5） -
科目： 来源： 题型：
查看答案和解析>>【题目】A，B两地相距60km，甲、乙两人从两地出发相向而行，甲先出发．图中
表示两人离A地的距离s（km）与时间t（h）的关系，请结合图象解答下列问题：（1）表示乙离A地的距离与时间关系的图象是 （填
或
）；（2）甲的速度是 km/h，乙的速度是 km/h；
（3）甲出发多少小时两人恰好相距5km？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），是两个全等的直角三角形（直角边分别为a，b，斜边为c）．
（1）用这样的两个三角形构造成如图（2）的图形（B，E，C三点在一条直线上），利用这个图形，求证：
．（2）当a=1，b=2时，将其中一个直角三角形放入平面直角坐标系中（如图（3）），使直角顶点与原点重合，两直角边a，b分别与x轴、y轴重合．请在坐标轴上找一点C，使△ABC为等腰三角形．
①写出一个满足条件的在x轴上的点的坐标： ；
②写出一个满足条件的在y轴上的点的坐标： ；
③满足条件的在y轴上的点共有 个．
-
科目： 来源： 题型：
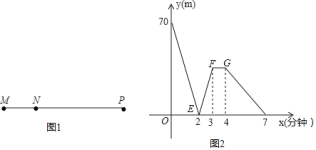
查看答案和解析>>【题目】科技小组进行了机器人行走性能试验，如图1，甲，乙两机器人分别从M，N两点同时同向出发，经过7分钟，甲，乙同时到达P点，乙机器人始终以60米/分的速度行走，图2是甲，乙两机器人之间的距离y（米）与他们的行走时间x（分钟）之间的函数图象，请结合图形，回答下列问题：
（1）M，N两点之间的距离是 米
（2）求出M，P两点之间的距离（写出解答过程）；
（3）求甲前2分钟的速度（写出解答过程）；
（4）若前3分钟甲的速度不变，图2中，点F的坐标为 ；
（5）若线段FG∥x轴，则此段时间内甲的速度为 米/分；
-
科目： 来源： 题型：
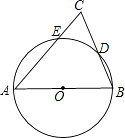
查看答案和解析>>【题目】如图，AB为⊙O的直径，AC交⊙O于E点，BC交⊙O于D点，CD=BD，∠C=70°．现给出以下四种结论：①∠A=45°；②AC=AB；③AE=BE；④CEAB=2BD2 ． 其中正确结论的序号是（ ）
A.①②
B.②③
C.②④
D.③④
相关试题
