【题目】完成下面的证明:
已知:如图,点 D,E,F 分别在线段 AB,BC,AC 上,连接 DE、EF,DM 平分∠ADE 交 EF 于点 M,∠1+∠2=180°. 求证:∠B =∠BED.
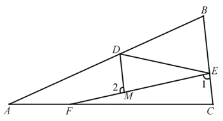
证明:∵∠1+∠2=180°(已知),
又∵∠1+∠BEM=180°(平角定义),
∴∠2=∠BEM( ),
∴DM∥ ( ).
∴∠ADM =∠B( ),
∠MDE =∠BED( ).
又∵DM 平分∠ADE (已知),
∴∠ADM =∠MDE (角平分线定义).
∴∠B =∠BED( ).
参考答案:
【答案】见解析
【解析】
根据平行线的判定与性质、同角或等角的补角相等求解可得.
证明:∵∠1+∠2=180°(已知),
又∵∠1+∠BEM=180°(平角定义),
∴∠2=∠BEM(同角的补角相等),
∴DM∥BC(同位角相等两直线平行).
∴∠ADM=∠B(两直线平行同位角相等),
∠MDE=∠BED(两直线平行内错角相等).
又∵DM平分∠ADE(已知),
∴∠ADM=∠MDE(角平分线定义).
∴∠B=∠BED(等量代换).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知一次函数y=﹣x+b与反比例函数y=
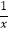 的图象有2个公共点,则b的取值范围是( )
的图象有2个公共点,则b的取值范围是( )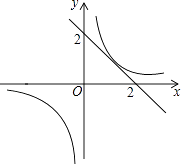
A.b>2
B.﹣2<b<2
C.b>2或b<﹣2
D.b<﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),…, 则第 200 个点的横坐标为_________.

-
科目: 来源: 题型:
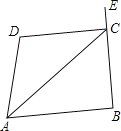
查看答案和解析>>【题目】如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°
(1)∠DCA的度数;
(2)∠DCE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )

A. 2B.
 C. 4D.
C. 4D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知O为直线BC上一定点,点A在直线外一定点.在直线BC上取点P,使得以O、A、P为顶点的三角形为等腰三角形.
(1)当∠AOC=30°时,如果我们通过分类讨论、画图尝试可以找到满足条件的点P共有______个.
(2)若在直线BC上有且只有两个满足条件的点P,则∠AOC=______.

相关试题

