搜索
【题目】在△ABC中，∠ACB=90°，AC=BC=4，点D为AB的中点，M，N分别在BC，AC上，且BM=CN现有以下四个结论：
①DN=DM； ② ∠NDM=90°； ③ 四边形CMDN的面积为4； ④△CMN的面积最大为2.
其中正确的结论有（ ）
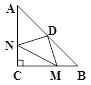
A. ①②④； B. ①②③； C. ②③④； D. ①②③④.
参考答案：
【答案】D
【解析】连接CD，
∵在△ABC中，∠ACB=90°，AC=BC=4，点D为AB的中点，
∴∠B=∠NCD=45°，CD=BD，∠CDB=90°，S△CDB=
S△ABC=
·
AC·BC=
=4 ，
又∵BM=CN，
∴△DBM≌△DCN，
∴DN=DM，∠CDN=∠DBM，S△CDN=S△DBM，
∴∠DMN=∠CDN+∠CDM=∠CDM+∠BDM=∠CDB=90°，
S四边形CMDN=S△CDN+S△CDM= S△BDM+S△CDM=S△CBD=4.
∵S△CMN+S△DMN= S四边形CMDN=4，
∴当S△DMN最小时，S△CMN的面积最大，
∴当DM⊥BC时，DM=DN=2，此时S△DMN最小=2，
∴此时，S△CMN的面积最大=4-2=2.
综上所述，上述四个结论全都正确.
故选D.
-
科目： 来源： 题型：
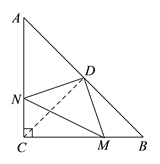
查看答案和解析>>【题目】如图，⊙O中，直径CD⊥弦AB于E，AM⊥BC于M，交CD于N，连AD．
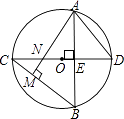
（1）求证：AD=AN；
（2）若AB=4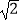
，ON=1，求⊙O的半径． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P，若∠BPC＝40°，则∠CAP＝（ ）
A. 40°B. 45°C. 50°D. 60°
-
科目： 来源： 题型：
查看答案和解析>>【题目】《算法统宗》是中国古代数学名著，作者是我国明代数学家程大位．在《算法统宗》中记载：“以绳测井，若将绳三折测之，绳多4尺，若将绳四折测之，绳多1尺，绳长井深各几何？”
译文：“用绳子测水井深度，如果将绳子折成三等份，井外余绳4尺；如果将绳子折成四等份，井外余绳1尺．问绳长、井深各是多少尺？”
设井深为x尺，根据题意列方程，正确的是（ ）
A. 3（x+4）=4（x+1） B. 3x+4=4x+1
C. 3（x﹣4）=4（x﹣1） D.
-
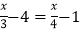
科目： 来源： 题型：
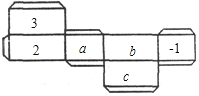
查看答案和解析>>【题目】如图是一个长方体纸盒的平面展开图，已知纸盒中相对两个面上的数互为相反数．
（1）填空：a=______，b=______，c=______．
（2）先化简，再求值：-a2b+2（3ab2-a2b）-3（2ab2-a2b）+abc
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）计算：[（x+y）2﹣（x﹣y）2]÷（2xy）．
（2）解方程：
（3）因式分解：xy2﹣4x
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点O是正方形ABCD对角线BD的中点．
（1）如图1，若点E是OD的中点，点F是AB上一点，且使得∠CEF=90°，过点E作ME∥AD，交AB于点M，交CD于点N．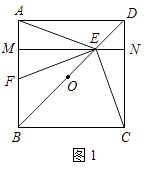
①∠AEM=∠FEM； ②点F是AB的中点；
（2）如图2，若点E是OD上一点，点F是AB上一点，且使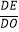
= 
= 
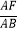，请判断△EFC的形状，并说明理由；
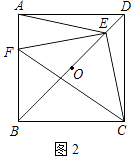
（3）如图3，若E是OD上的动点（不与O，D重合），连接CE，过E点作EF⊥CE，交AB于点F，当
= 
时，请猜想 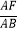的值（请直接写出结论）．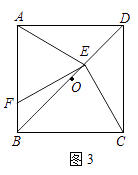
相关试题
