【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.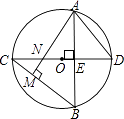
(1)求证:AD=AN;
(2)若AB=4 ![]() ,ON=1,求⊙O的半径.
,ON=1,求⊙O的半径.
参考答案:
【答案】
(1)证明:∵∠BAD与∠BCD是同弧所对的圆周角,
∴∠BAD=∠BCD,
∵AE⊥CD,AM⊥BC,
∴∠AMC=∠AEN=90°,
∵∠ANE=∠CNM,
∴∠BCD=∠BAM,
∴∠BAM=BAD,
在△ANE与△ADE中,
∵ 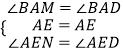 ,
,
∴△ANE≌△ADE,
∴AD=AN;
(2)解:∵AB=4 ![]() ,AE⊥CD,
,AE⊥CD,
∴AE=2 ![]() ,
,
又∵ON=1,
∴设NE=x,则OE=x﹣1,NE=ED=x,r=OD=OE+ED=2x﹣1
连结AO,则AO=OD=2x﹣1,
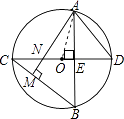
∵△AOE是直角三角形,AE=2 ![]() ,OE=x﹣1,AO=2x﹣1,
,OE=x﹣1,AO=2x﹣1,
∴(2 ![]() )2+(x﹣1)2=(2x﹣1)2,解得x=2,
)2+(x﹣1)2=(2x﹣1)2,解得x=2,
∴r=2x﹣1=3.
【解析】(1)先根据圆周角定理得出∠BAD=∠BCD,再由直角三角形的性质得出∠ANE=∠CNM,故可得出∠BCD=∠BAM,由全等三角形的判定定理得出△ANE≌△ADE,故可得出AD=AN;
(2)先根据垂径定理求出AE的长,设NE=x,则OE=x-1,NE=ED=x,r=OD=OE+ED=2x-1,连结AO,则AO=OD=2x-1,在Rt△AOE中根据勾股定理可得出x的值,进而得出⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场元旦期间对所有商品进行优惠促销优惠方案是:一次性购商品不超过1000元,不享受优惠;一次性购商品超过1000元但不超过2000元一律打九折;一次性购商品2000元以上一律打八折.
 如果小明一次性购商品的原价为2500元,那么他实际付款______元
如果小明一次性购商品的原价为2500元,那么他实际付款______元
 如果小华同学一次性购商品付款1620元,那么小华所购商品的原价为多少元?
如果小华同学一次性购商品付款1620元,那么小华所购商品的原价为多少元? -
科目: 来源: 题型:
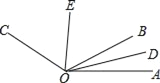
查看答案和解析>>【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=( )

A. 40°B. 45°C. 50°D. 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )

A. 3(x+4)=4(x+1) B. 3x+4=4x+1
C. 3(x﹣4)=4(x﹣1) D.
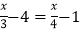
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M,N分别在BC,AC上,且BM=CN现有以下四个结论:
①DN=DM; ② ∠NDM=90°; ③ 四边形CMDN的面积为4; ④△CMN的面积最大为2.
其中正确的结论有( )
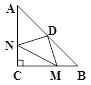
A. ①②④; B. ①②③; C. ②③④; D. ①②③④.
相关试题

