【题目】A、B、C三瓶不同浓度的酒精,A瓶内有酒精2kg,浓度x%,B瓶有酒精3kg,浓度y%,C瓶有酒精5kg,浓度z%,从A瓶中倒出10%,B瓶中倒出20%,C瓶中倒出24%,混合后测得浓度33.5%,将混合后的溶液倒回瓶中,使它们恢复原来的质量,再从A瓶倒出30%,B瓶倒出30%,C瓶倒出30%,混合后测得浓度为31.5%,测量发现![]() ,
,![]() ,
,![]() ,且x、y、z均为整数,则把起初A、B两瓶酒精全部混合后的浓度为______.
,且x、y、z均为整数,则把起初A、B两瓶酒精全部混合后的浓度为______.
参考答案:
【答案】![]()
【解析】
根据第一次A、B、C各取出部分混合后的浓度得到一条关于xyz的等式,再算出混合液倒回后A、B、C中后各自的酒精量,然后根据第二次混合再得到一条关于xyz的等式,联立组成方程组,使用x、y表示z,根据x、y、z的取值范围确定其准确整数值即可求解.
解:A瓶倒出10%:2000×10%=200(克),剩余:2000-200=1800(克),
B瓶倒出20%:3000×20%=600(克),剩余:3000-600=2400(克),
C瓶倒出24%:5000×24%=1200(克),剩余:5000-1200=3800(克),
根据题意得:(200×x%+600×y%+1200×z%)÷(200+600+1200)=33.5%,
混合液倒回后A瓶内的酒精量:1800×x%+200×33.5%,
混合液倒回后B瓶内的酒精量:2400×y%+600×33.5%,
混合液倒回后C瓶内的酒精量:3800×z%+1200×33.5%,
再根据题意可得:
[(1800×x%+200×33.5%)×30%+(2400×y%+600×33.5%)×30%+(3800×z%+1200×33.5%)×30%]÷(2000×30%+3000×30%+5000×30%)=31.5%,
整理组成方程组得:![]() ,
,
解得: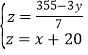 ,
,
∵![]() ,
,![]() ,
,
∴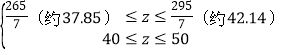 ,又∵
,又∵![]() 且为整数,
且为整数,
则![]() ,
,
代入可得: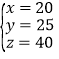 ,或者
,或者 或者
或者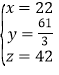 ,
,
∵x、y、z均为整数,则只有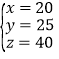 符合题意,
符合题意,
则把起初A、B两瓶酒精混合后的浓度为:![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=45°,AB=
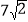 ,AC=6,点D,E为边AC上的点,AD=1,CE=2,点F为线段DE上一点(不与D,E重合),分别以点D、E为圆心,DF、EF为半径作圆.若两圆与边AB,BC共有三个交点时,线段DF长度的取值范围是_______.
,AC=6,点D,E为边AC上的点,AD=1,CE=2,点F为线段DE上一点(不与D,E重合),分别以点D、E为圆心,DF、EF为半径作圆.若两圆与边AB,BC共有三个交点时,线段DF长度的取值范围是_______. 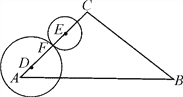
-
科目: 来源: 题型:
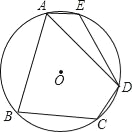
查看答案和解析>>【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在
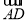 上.
上.(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 、
、 两地相距
两地相距 ,甲、乙两车分别沿同一条路线从
,甲、乙两车分别沿同一条路线从 地出发驶往
地出发驶往 地,已知甲车的速度为
地,已知甲车的速度为 ,乙车的速度为
,乙车的速度为 ,甲车先出发
,甲车先出发 后乙车再出发,乙车到达
后乙车再出发,乙车到达 地后再原地等甲车.
地后再原地等甲车.(1)求乙车出发多长时间追上甲车?
(2)求乙车出发多长时间与甲车相距
 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3-1),B(-4,-3),C(-2,-3).
(1)画出将△ABC向上平移5个单位得到的△A1B1C1,并写出点B1的坐标;
(2)画出△ABC关于点O成中心对称的图形△A2B2C2,并写出点B2的坐标;
(3)观察图形,△A1B1C1和△A2B2C2成中心对称吗?如果成中心对称,那么对称中心的坐标为_____;如果不成中心对称,请说明理由.

-
科目: 来源: 题型:
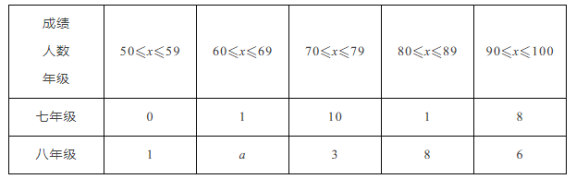
查看答案和解析>>【题目】为引导学生广泛阅读文学名著,某校在七年级、八年级开展了读书知识竞赛.该校七、八年级各有学生400人,各随机抽取20名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
七年级:
74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
八年级:
76 88 93 65 78 94 89 68 95 50 89 88 89 89 77 94 87 88 92 91
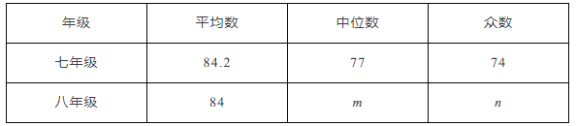
平均数、中位数、众数如表所示:
根据以上信息,回答下列问题:
(1)
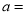 ______,
______,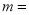 ______,
______,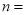 ______;
______;(2)该校对读书知识竞赛成绩不少于80分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有______人;
(3)结合以上数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如下图所示:

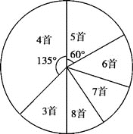
大赛结束后一个月,再次调查这部分学生“一周诗词诵背数量”,绘制成统计表:
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人 数
10
10
15
m
25
20
请根据调查的信息
(1)本次调查抽取了多少名学生?
(2)补全条形统计图,在扇形统计图中,“6首”的圆心角为 度;
(3)表格中m的值为 ;
(4)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
相关试题

