【题目】请认真阅读材料,并解决下面问题:
(1)以 a 、b 为直角边,以 c 为斜边做四个全等的直角三角形,把这四个直角三角形拼成如图所示形状,使 A 、 E 、 B 三点在一条直线上, B 、 F 、C 三点在一条直线上, C 、G 、D 三点在一条直线上。容易得到:四边形 ABCD 和四边形 EFGH 均是正方形;请用两个不同的代数式 和 表示正方形ABCD 的面积;于是可得到直角三角形关于三边的一个重要的等量关系是 (用含字母 a 、b 、 c 的最简式子填空)
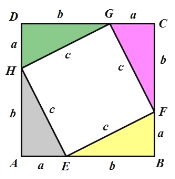
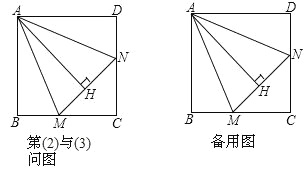
(2)如图,已知正方形 ABCD 中,MAN 45 ,MAN 绕点A 顺时针旋转,它的两边分别交CB 、DC 于点 M 、 N , AH MN 于点 H 。请问: MN 与BM 、 DN 之间有何数量关系?请说明理由;
(3)如图,在(2)的情况下,
①请判断 AH 与 AB 之间的数量关系,并说明理由;
②已知 AH 12 ,若 N 还是CD 的中点,结合(1)的结论,求 BM 的长。
参考答案:
【答案】(1) (a+b)2,2ab+c2,c2=a2+b2; (2)见详解;(3)①AB=AH;②4.
【解析】
(1)根据正方形ABCD的面积等于边长的平方或者等于4个全等的直角三角形与正方形EFGH的面积和,可列出不同的代数式,根据代数式可得等量关系式;
(2)延长CB,使BE=DN,连接AE,由题意可证△ABE≌△ADN,可得AE=AN,∠EAB=∠DAN,可得∠EAM=∠MAN=45°,即可证△EAM≌△NAM,
即可得MN=DN+BM;
(3)①由△EAM≌△NAM,可得S△EAM=S△NAM,即![]() ×EM×AB=
×EM×AB=![]() ×MN×AH,且EM=MN,可得AB=AH;
×MN×AH,且EM=MN,可得AB=AH;
②由题意可求BC=AB=CD=12,CN=DN=BE=6,根据勾股定理可求BM的长.
解:(1)∵正方形ABCD的面积=(a+b)2,正方形ABCD的面积=4×![]() ab+c2=c2+2ab
ab+c2=c2+2ab
∴c2=a2+b2
故答案为:(a+b)2,2ab+c2,c2=a2+b2.
(2)MN=BM+DN
如图:延长CB,使BE=DN,连接AE
∵四边形ABCD是正方形
∴AB=AD=BC=CD,∠ADC=∠ABC=∠BCD=90°=∠BAD
∵BE=DN,AB=AD,∠ADC=∠ABE
∴△ABE≌△ADN(SAS)
∴AE=AN,∠EAB=∠DAN
∵∠MAN=45°,∠BAD=90°
∴∠BAM+∠DAN=45°
∴∠BAM+∠EAB=45°
∴∠EAM=∠MAN,且AM=AM,AE=AN
∴△EAM≌△NAM(SAS)
∴MN=EM
∵EM=BM+BE=BM+DN
∴MN=BM+DN
(3)①∵△EAM≌△NAM
∴S△EAM=S△NAM
∴![]() ×EM×AB=
×EM×AB=![]() ×MN×AH,且EM=MN
×MN×AH,且EM=MN
∴AB=AH
②∵AH=12,
∴AB=12
∴CD=BC=12
∵点N是CD的中点
∴CN=DN=BE=6
∴MN=BM+6
在Rt△MNC中,MN2=CM2+CN2.
∴(BM+6)2=(12-BM)2+36
∴BM=4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
 的图象与一次函数y=kx+m的图象相交于点A(2,1).
的图象与一次函数y=kx+m的图象相交于点A(2,1).(1)分别求出这两个函数的解析式;
(2)当x取什么范围时,反比例函数值大于0;
(3)若一次函数与反比例函数另一交点为B,且纵坐标为﹣4,当x取什么范围时,反比例函数值大于一次函数的值;
(4)试判断点P(﹣1,5)关于x轴的对称点P′是否在一次函数y=kx+m的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(组)与不等式(组)是代数的重要组成部分,也是解决数学问题的重要工具,请利用所学,解决以下 3 个问题:
(1)当 k 为何整数时,关于 x , y 的方程组
 的解满足 x y 且 x y 4 ;
的解满足 x y 且 x y 4 ;(2)已知正整数 a ,使得关于 x , y 的方程组
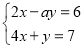 的解是整数,解关于 x 的不等式
的解是整数,解关于 x 的不等式 ;
;(3)已知 x ,y ,z 为 3 个非负实数,且满足3x 2 y z 5 ,x y z 2 ,记 S 2x y z对于符合题意的任意实数 S ,不等式 2m S 3 始终成立,试确定 m 的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(5分)某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负):

⑴根据记录可知前三天共生产________辆;
⑵产量最多的一天比产量最少的一天多生产________辆;
⑶该厂实行计件工资制,每辆车60元,超额完成任务每辆奖15元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个问题解决往往经历发现猜想——探索归纳——问题解决的过程,下面结合一道几何题来体验一下.
(发现猜想)(1)如图①,已知∠AOB=70°,∠AOD=100°,OC为∠BOD的角平分线,则∠AOC的度数为 ;.
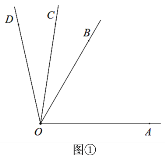
(探索归纳)(2)如图①,∠AOB=m,∠AOD=n,OC为∠BOD的角平分线. 猜想∠AOC的度数(用含m、n的代数式表示),并说明理由.
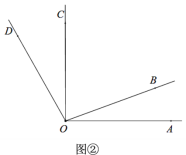
(问题解决)(3)如图②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射线OB绕点O以每秒20°逆时针旋转,射线OC绕点O以每秒10°顺时针旋转,射线OD绕点O每秒30°顺时针旋转,三条射线同时旋转,当一条射线与直线OA重合时,三条射线同时停止运动. 运动几秒时,其中一条射线是另外两条射线夹角的角平分线?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市水果批发部门欲将 A 市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为 200 元/ 时.其它主要参考数据如下:
运输工具
途中平均速度(千米/ 时)
运费(元/ 千米)
装卸费用(元)
火车
100
15
2000
汽车
80
20
900
运输过程中,火车因多次临时停车,全程在路上耽误 2 小时 45 分钟,火车的总支出费用与汽车的总支出费用相同,请问某市与本地的路程是多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)对于任意正实数a、b,
∵(
 ﹣
﹣ )2≥0,
)2≥0,∴a﹣2
 +b≥0,
+b≥0,∴a+b≥2
 ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2 ).
).(1)(获得结论)在a+b≥2
 (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,则a+b≥2
 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2 .
.根据上述内容,回答下列问题:若m>0,只有当m= 时,m+
 有最小值 .
有最小值 .(2)(探索应用)已知点Q(﹣3,﹣4)是双曲线y=
 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y= (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.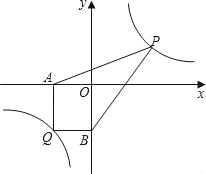
相关试题

