【题目】如图,AB的中垂线为CP交AB于点P,且AC=2CP.甲、乙两人想在AB上取D、E两点,使得AD=DC=CE=EB,其作法如下:甲作∠ACP、∠BCP的角平分线,分别交AB于D、E两点,则D、E即为所求;乙作AC、BC的中垂线,分别交AB于D、E两点,则D、E即为所求.对于甲、乙两人的作法,下列正确的是( )
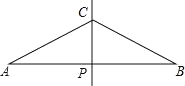
A.两人都正确 B.两人都错误
C.甲正确,乙错误 D.甲错误,乙正确
参考答案:
【答案】A.
【解析】
试题解析: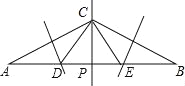
甲、乙都正确,
理由是:∵CP是线段AB的垂直平分线,
∴BC=AC,∠APC=∠BPC=90°,
∵AC=2CP,
∴∠A=30°,
∴∠ACP=60°,
∵CD平分∠ACP,
∴∠ACD=![]() ∠ACP=30°,
∠ACP=30°,
∴∠ACD=∠A,
∴AD=DC,
同理CE=BE,
即D、E为所求;
∵D在AC的垂直平分线上,
∴AD=CD,
同理CE=BE,
即D、E为所求,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-xy)3·(7xy2-9x2y)的结果正确的是( )
A. -7x2y5+9x3y4 B. 7x2y5-9x3y4 C. -7x4y5+9x5y4 D. 7x4y5+9x5y4
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算﹣2+6等于( )
A. 4 B. 8 C. ﹣4 D. ﹣8
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,BD是一条对角线,点P在CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QM⊥BD于M,连接AM,PM(如图1).

(1)判断AM与PM的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,其它条件不变(如图2),(1)中的结论是否仍成立?请说明理由.
-
科目: 来源: 题型:
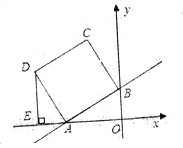
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=0.5x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,过点D作DE⊥x轴,垂足为E.
(1)求点A、B的坐标,并求边AB的长;
(2)求点D的坐标;
(3)你能否在x轴上找一点M,使△MDB的周长最小?如果能,请求出M点的坐标;如果不能,说明理由.
-
科目: 来源: 题型:
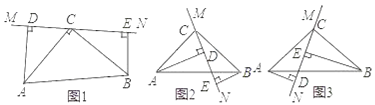
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算x(x2-1)+2x2(x+1)-3x(2x-5)的结果是( )
A. 3x3-4x2+14xB. 3x3-4x2+14xC. 3x3-4x2+14xD. 3x3-4x2+14x
相关试题

