【题目】如图,△ABC中,AB=AC,AD是BC边上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE是矩形;
(2)若BC=6,∠DOC=60°,求四边形ADCE的面积.

参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据平行四边形的性质得出四边形ADCE是平行四边形,根据垂直推出∠ADC=90°,根据矩形的判定得出即可;
(2)依据等腰三角形三线合一的性质可求得DC,然后证明△OCD为等边三角形,从而可求得AC的长,然后依据勾股定理可求得AD的长,最后利用矩形的面积公式求出即可.
(1)证明:∵点O是AC中点,
∴OA=OC,
又∵OE=OD,
∴四边形ADCE是平行四边形.
∵AD是BC边上的高,
∴∠ADC=90°,
∴四边形ADCE的是矩形.
(2)解:∵AD是等腰三角形BC边上的高,BC=6,
∴BD=DC=3
∵四边形ADCE的是矩形,
∴OD=OC=![]() AC.
AC.
∵∠DOC=60°,
∴△DOC是等边三角形,
∴OC=DC=3,
∴AC=6.
在Rt△ADC中,∠ADC=90°,DC=3,AC=6,
由勾股定理得 AD=![]() ,
,
∴四边形ADCE的面积S=AD×DC=3×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
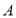 、
、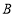 两地相距
两地相距 ,甲、乙两车分别从
,甲、乙两车分别从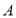 、
、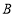 两地同时出发,相向而行.已知甲车速度为
两地同时出发,相向而行.已知甲车速度为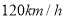 ,乙车速度为
,乙车速度为 ,经过
,经过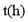 后两车相距
后两车相距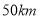 ,则
,则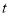 的值是( )
的值是( )A.2B.10C.2或10D.2或2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商家今年3月份两次同时购进了甲、乙两种不同单价的糖果,第一次购买甲种糖果的数量比乙种糖果的数量多50%,第二次购买甲种糖果的数量比第一次购买甲种糖果的数量少60%,结果第二次购买糖果的总数量虽然比第一次购买糖果的总数量多20%,但第二次购买甲乙糖果的总费用却比第一次购买甲乙糖果的总费用费少10%.(甲,乙两种糖果的单价不变),则乙种糖果的单价是甲种糖果单价的_____%.
-
科目: 来源: 题型:
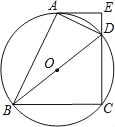
查看答案和解析>>【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆格力厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸r的范围为176≤r≤185的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据
级别
频数
165.5~
170.5
170.5~
175.5
175.5~
180.5
180.5~
185.5
185.5
~190.5
190.5~
195.5
甲车间
2
4
a
b
2
1
乙车间
1
2
9
6
2
0
分析数据:
车间
平均数
众数
中位数
方差
甲车间
180
185
180
43.1
乙车间
180
180
c
22.6
应用数据
(2)请写出表中a= ,b= ,c= mm.
(2)估计甲车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AC:y=
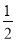 x+2分别交x轴和y轴于A,C两点,直线BD:y=﹣x+b分别交x轴和y轴于B,D两点,直线AC与BD交于点E,且OA=OB.
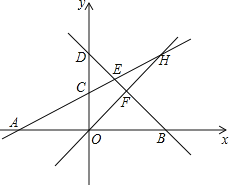
x+2分别交x轴和y轴于A,C两点,直线BD:y=﹣x+b分别交x轴和y轴于B,D两点,直线AC与BD交于点E,且OA=OB.(1)求直线BD的解析式和E的坐标.
(2)若直线y=x分别与直线AC,BD交于点H和F,求四边形ECOF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大课间是学校的校体课程之一,涉及的范围广,内容繁多。某校根据实际情况决定开设
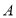 :乒乓球,
:乒乓球,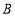 :篮球,
:篮球,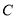 :跑步,
:跑步,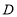 :跳绳四种运动项目,为了了解学生最喜欢哪一项运动,随机抽取了600名学生进行调查,并将调查结果绘制成如下的统计图,结合图中信息解答下列问题:
:跳绳四种运动项目,为了了解学生最喜欢哪一项运动,随机抽取了600名学生进行调查,并将调查结果绘制成如下的统计图,结合图中信息解答下列问题:
(1)补全条形统计图;
(2)制作扇形统计图;
(3)若该校有学生2400人,请问:喜欢打乒乓球的学生人数大约有多少人?
相关试题

