Question

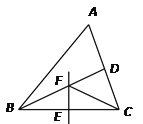
【题目】如图，在△ABC中，BD平分∠ABC，BC的垂直平分线交BC于点E，交BD于点F，连结CF．若∠A=60°，∠ACF =45°，则∠ABC的度数为（ ）

A. 45° B. 50° C. 55° D. 60°

Answer 1

【答案】B

【解析】 设∠ABD=∠CBD=x°，则∠ABC=2x°，根据线段垂直平分线性质求出BF=CF，推出∠FCB=∠CBD，根据三角形内角和定理得出方程，求出方程的解即可．

解：∵BD平分∠ABC，

∴∠ABD=∠CBD，

设∠ABD=∠CBD=x°，则∠ABC=2x°，

∵EF是BC的垂直平分线，

∴BF=CF，

∴∠FCB=∠CBD=x°，

∵∠A=60°，∠ACF=45°，

∴60°+45°+x°+2x°=180°，

解得：x=25，

∴∠ABC=2x°=50°，

故选B．

“点睛”本题考查了三角形内角和定理，线段垂直平分线性质的应用，能求出BF=CF是解此题的关键，注意线段垂直平分线上的点到线段两个端点的距离相等.