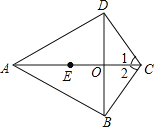
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.
(1)求证:∠1=∠2;
(2)连结BE、DE,判断四边形BCDE的形状,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)四边形BCDE是菱形,理由见解析.
【解析】
试题分析:(1)证明△ADC≌△ABC后利用全等三角形的对应角相等证得结论.
(2)首先判定四边形BCDE是平行四边形,然后利用对角线垂直的平行四边形是菱形判定菱形即可.
试题解析:解:(1)证明:∵在△ADC和△ABC中,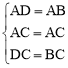 ,
,
∴△ADC≌△ABC(SSS).∴∠1=∠2.
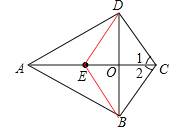
(2)四边形BCDE是菱形,理由如下:
如答图,∵∠1=∠2,DC=BC,∴AC垂直平分BD.
∵OE=OC,∴四边形DEBC是平行四边形.
∵AC⊥BD,∴四边形DEBC是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),点P是等腰三角形ABC底边BC上的一动点,过点P作BC的垂线,交直线AB于点Q,交CA的延长线于点R.

(1)请观察AR与AQ,它们相等吗?并证明你的猜想.
(2)如图(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图(2)中完成图形,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
(2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点B,C是x轴上的两个定点,∠ACB=90°,AC=BC,点A(l,3),点P是x轴上的一个动点,点E是AB的中点,在△PEF中,∠PEF=90°,PE=EF
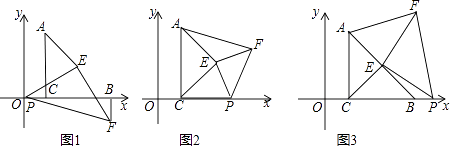
(1)如图1,当点P与坐标原点重合时:①求证△PCE≌△FBE;②求点F的坐标;
(2)如图2,当点P在线段CB上时,求证S△CPE=S△AEF
(3)如图3,当点P在线段CB的延长线时,若S△AEF=4S△PBE则此刻点F的坐标为 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2 – 7x+6 = 0的一次项系数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式3x﹣1>﹣4的最小整数解是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(-2xy)(3x2y-2x+1)=_________.
相关试题

