【题目】如图，点C为线段AB上一点，△DAC、△ECB都是等边三角形，AE、DC交于点M，DB、EC交于点N，DB、AE交于点P，连接MN，下列说法中正确的个数有（ ）

①MN∥AB；②∠DPM＝60°；③∠DAP＝∠PEC；④△ACM≌△DCN；⑤若∠DBC＝30°，则∠AEB＝80°

A.2个B.3个C.4个D.5个

参考答案：

【答案】C

【解析】

根据题目中的信息和等边三角形的性质，再应用三角形全等的方法逐个判断即可.

∵△DAC、△ECB都是等边三角形，

∴AC=CD，BC=CE，∠ACD=∠BCE=60°，

∴∠ADC=∠DCE=60°，

∴AD∥CE，∴∠DAP=∠PEC，故③正确；

在△ACE与△BCD中，

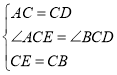
∴△ACE≌△BCD，∴∠CAE=∠CDB，

∵∠PMD=∠AMC，∴∠DPM=∠ACM=60°，故②正确，

在△ACM与△DCN中，

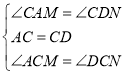
∴△ACM≌△DCN，故④正确；

∴CM=CN，∴△CMN是等边三角形，

∴∠CMN=60°，∴∠CMN=∠ACD，∴MN∥AB，故①正确；

∵∠DBC=30°，∴∠PBE=30°，

∵∠DPM=60°，∴∠BPE=60°，∴∠AEB=90°．故⑤错误；

正确的个数为4个，故选C．

关闭