【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过 点A,C 画一条射线AE,AE就是∠PRQ的平分线。此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE。则说明这两个三角形全等的依据是( )

A. SSS B. SAS C. ASA D. AAS
参考答案:
【答案】A
【解析】
在△ADC和△ABC中,由于AC为公共边,AB=AD,BC=DC,利用SSS定理可判定△ADC≌△ABC,进而得到∠DAC=∠BAC,即∠QAE=∠PAE.
在△ADC和△ABC中,
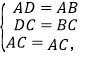
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的周长是16,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D且OD=2,△ABC的面积是________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.
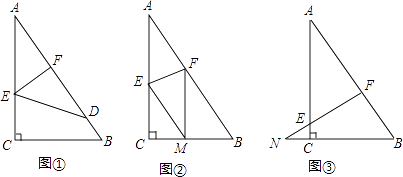
(1)图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF , 求AE的长;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE= ,求
,求  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F.试猜想EF、BE、CF之间有怎样的关系,并说明理由.


(2)如图,若将图①中∠ACB的平分线改为外角∠ACD的平分线,其它条件不变,则刚才的结论还成立吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B=40°,AD是BC边上的高,且∠DAC=20°,则∠BAC=________.
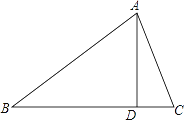
【答案】70°
【解析】∵∠B=40°,AD⊥BC,
∴∠BAD=90°-40°=50°.
∵∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°.
【题型】填空题
【结束】
16【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
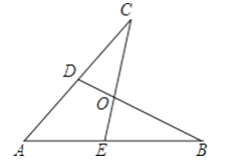
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
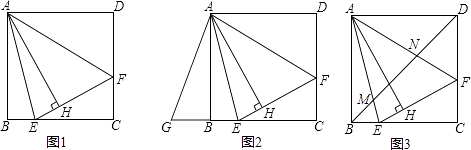
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC和△BDE都是等边三角形.则下列结论:①AE=CD;②BF=BG;③∠AHC=60°;④△BFG是等边三角形;⑤HB平分∠AHD.其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
相关试题

