【题目】如图所示,已知△ABC和△BDE都是等边三角形.则下列结论:①AE=CD;②BF=BG;③∠AHC=60°;④△BFG是等边三角形;⑤HB平分∠AHD.其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
参考答案:
【答案】D
【解析】
由题中条件可得△ABE≌△CBD,得出对应边、对应角相等,进而得出△BGD≌△BFE,△ABF≌△CGB,再由边角关系即可求解题中结论是否正确,进而可得出结论.
∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,![]()
∴∠ABE=∠CBD,
即AB=BC,BD=BE,∠ABE=∠CBD
∴△ABE≌△CBD,
∴S△ABE=S△CBD,AE=CD,∠BDC=∠AEB,
又∵![]()
∴△BGD≌△BFE,
∴BG=BF,![]()
故①②正确;
∵△ABE≌△CBD,
∴∠EAB=∠BCD,
∵![]()
∴![]() ∴③正确;
∴③正确;
∵BF=BG,![]()
∴△BFG是等边三角形,∴④正确;
∴![]()
∴FG∥AD,
∵BF=BG,AB=BC,![]() ,
,
∴△ABF≌△CBG,
∴∠BAF=∠BCG,
∴![]()
∴![]()
∵![]()
∴B、G、H、F四点共圆,
∵FB=GB,
∴∠FHB=∠GHB,
∴BH平分∠GHF,
∴⑤正确;
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过 点A,C 画一条射线AE,AE就是∠PRQ的平分线。此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE。则说明这两个三角形全等的依据是( )

A. SSS B. SAS C. ASA D. AAS
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B=40°,AD是BC边上的高,且∠DAC=20°,则∠BAC=________.
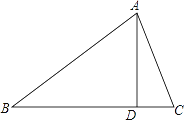
【答案】70°
【解析】∵∠B=40°,AD⊥BC,
∴∠BAD=90°-40°=50°.
∵∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°.
【题型】填空题
【结束】
16【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
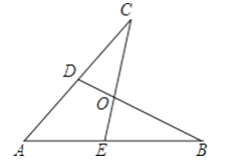
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
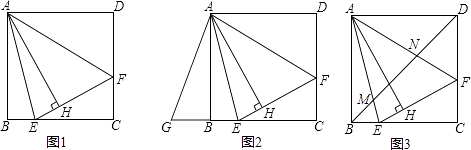
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.

(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(Ⅱ)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
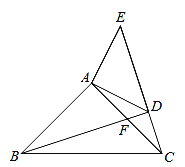
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径
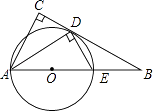
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB=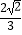 ,AE=4,求CD.
,AE=4,求CD.
相关试题

