Question

【题目】设四棱锥P﹣ABCD的底面不是平行四边形，用平面 α去截此四棱锥，使得截面四边形是平行四边形，则这样的平面α（ ）
A.不存在
B.只有1个
C.恰有4个
D.有无数多个

Answer 1

【答案】D
【解析】证明：由侧面PAD与侧面PBC相交，侧面PAB与侧面PCD相交， 设两组相交平面的交线分别为m，n，
由m，n决定的平面为β，
作α与β平行且与四条侧棱相交，
交点分别为A1 ， B1 ， C1 ， D1
则由面面平行的性质定理得：
A1B1∥m∥D1C1 ， A1D1∥n∥B1C1 ，
从而得截面必为平行四边形．
由于平面α可以上下移动，则这样的平面α有无数多个．
故选D．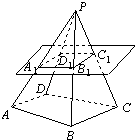

若要使截面四边形A1B1C1D1是平行四边形，我们只要证明A1B1∥C1D1 ， 同时A1D1∥B1C1即可，根据已知中侧面PAD与侧面PBC相交，侧面PAB与侧面PCD相交，根据面面平行的性质定理，我们易得结论．